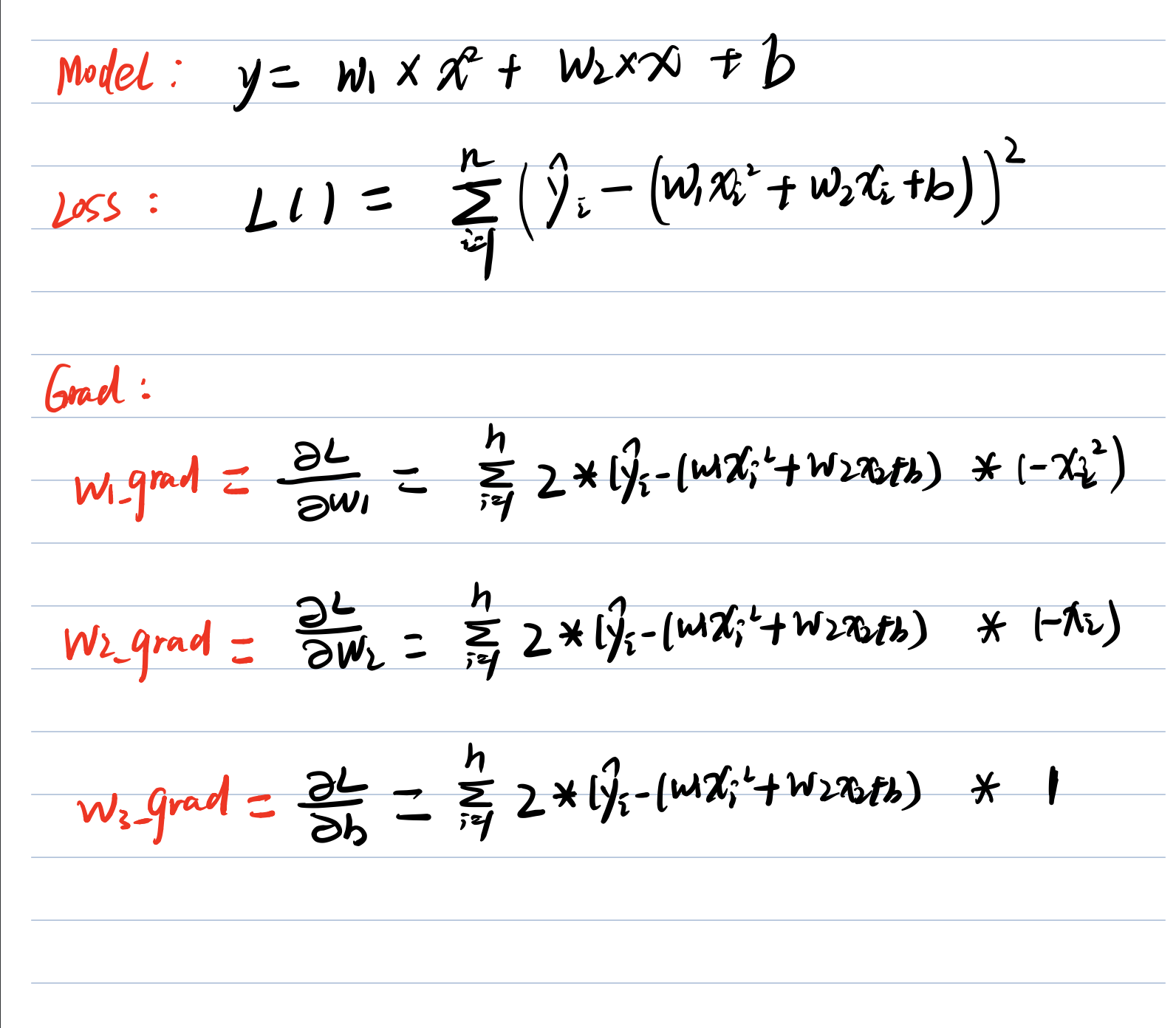Quartz 4

梯度下降法 ②_学习率

7 min read

入门系列文章： 深度学习入门系列一-梯度下降法 深度学习入门系列一-梯度下降法-② 梯度下降法3 深度学习入门系列4-反向传播BP算法 深度学习入门系列-逻辑回归 深度学习入门系列6-Convolution-Neural-Network-CNN-卷积神经网络 深度学习入门系列7-Tips-For-DeepLearning-全程高能 深度学习入门系列8-Tips-For-DeepLearning-2-全程高能

梯度下降法及其优化

在上一篇文章中深度学习入门系列一-梯度下降法已经讲述了梯度下降法的基本流程，也讲了梯度下降法存在的问题，这篇文章就来继续讲解梯度下降法的后续。

前一篇文章提到学习率的问题，如果学习率过大会导致震荡而难以收敛，过小的话又会收敛太慢，耗费时间，因此出现了Adagrad.

Tip1：Adaptive Learning Rate

学习率对于参数调整影响很大，因此需要仔细地调整，手动调节参数肯定是不太现实，而自适应的调整参数有以下两个原则：

  • 开始阶段学习率比较大
  • 随着迭代次数的增加越来越小

Adagrad Gradient Descent

与Gradient Descent的比较

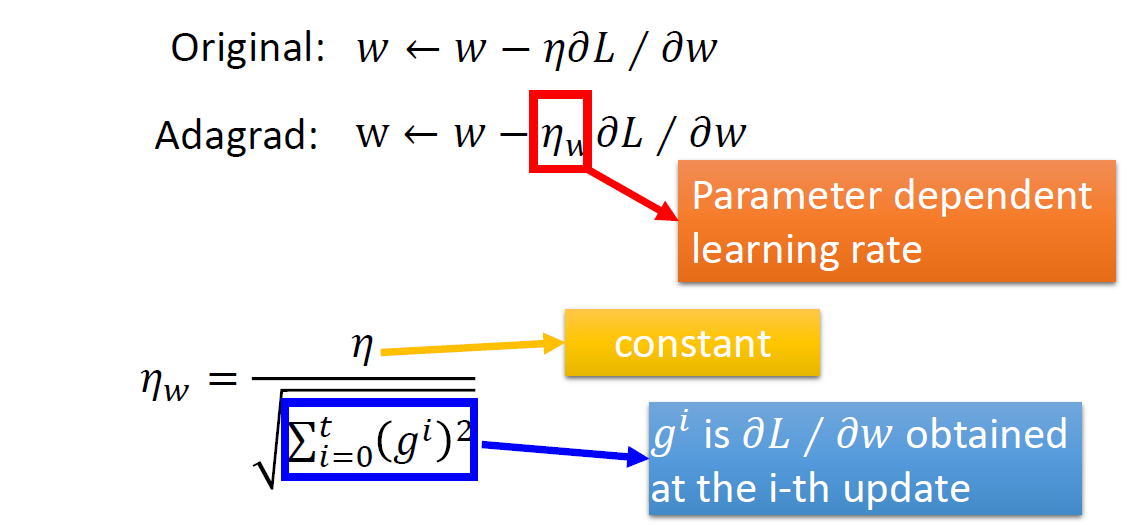
数学公式推导

原始学习率变成了 常数/梯度的平方和开根号，这个公式也是又推导过程的，如下(笔记字比较丑)：

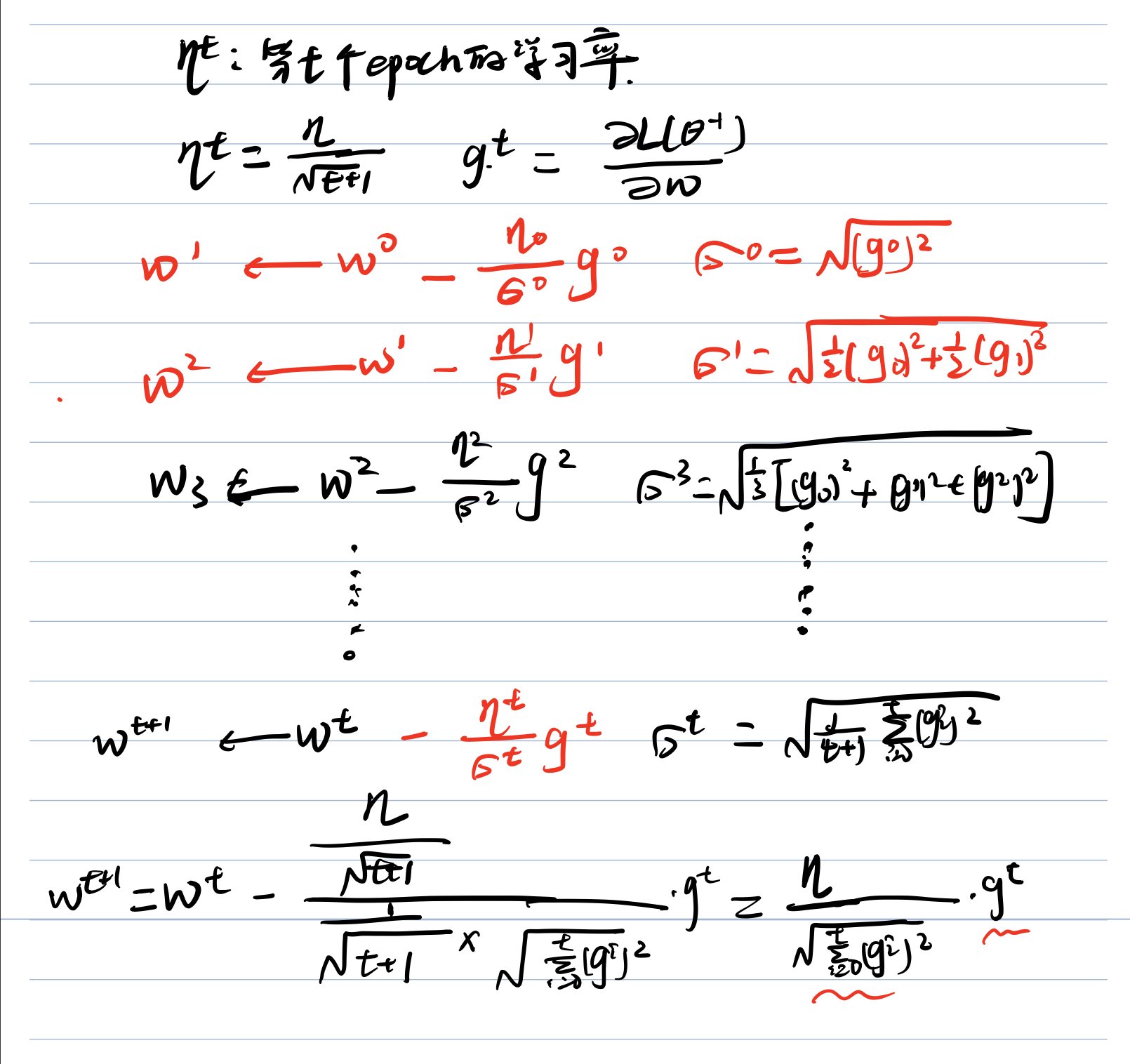
其中的矛盾

观察最后一步，可以看出后面的 **梯度 ** 和 **分母的梯度的平方和开根号 ** （最后一行红笔画出来的）是矛盾的，梯度越大，分母也会越大，约束整个函数，但是效果会比较好。这个可以解释为，不只是考虑了一阶偏导数g(t),同时也考虑了二阶偏导数，所以结果会更加准确。(具体的可以参考李宏毅深度学习视频，前一篇文章有提到。)

Adagrad总结

Adagrad梯度下降法其实是实现了自适应的去调节学习率，不在需要手动的仔细去调节。

Tip2：Stochastic Gradient Descent

随机梯度下降法也是比较常见的，是梯度下降法的一种变体，改变也不多，它与梯度下降法的不同之处在于：

​ 假设有十组训练数据，也就是十个函数，梯度下降法会把每一组参数带进去计算损失求和，每组参数的梯度也相应会进行求和嘛，然后才更新一次参数；随机梯度下降法不再需要求和这一过程，即随便一组数据带入损失函数求出梯度直接更新参数。

这种方法听起来也比较一般，它的主要优点在于更新参数快， 天下武功，唯快不破嘛。

Tip3：Feature scaling

特征归一化。在做梯度下降法时，只要梯度分不一样，可以归一化之后在做，主要是因为如果某一个特征值非常大，那么它所占的比重就会非常大，这对学习非常不利。

常用的一个归一化方法：

对于特征 x1,x2,x3······xn,每种特征的某一个维度求一下这列数的均值和标准差，然后原始数据减去均值除以标准差即可归一化，如下图：

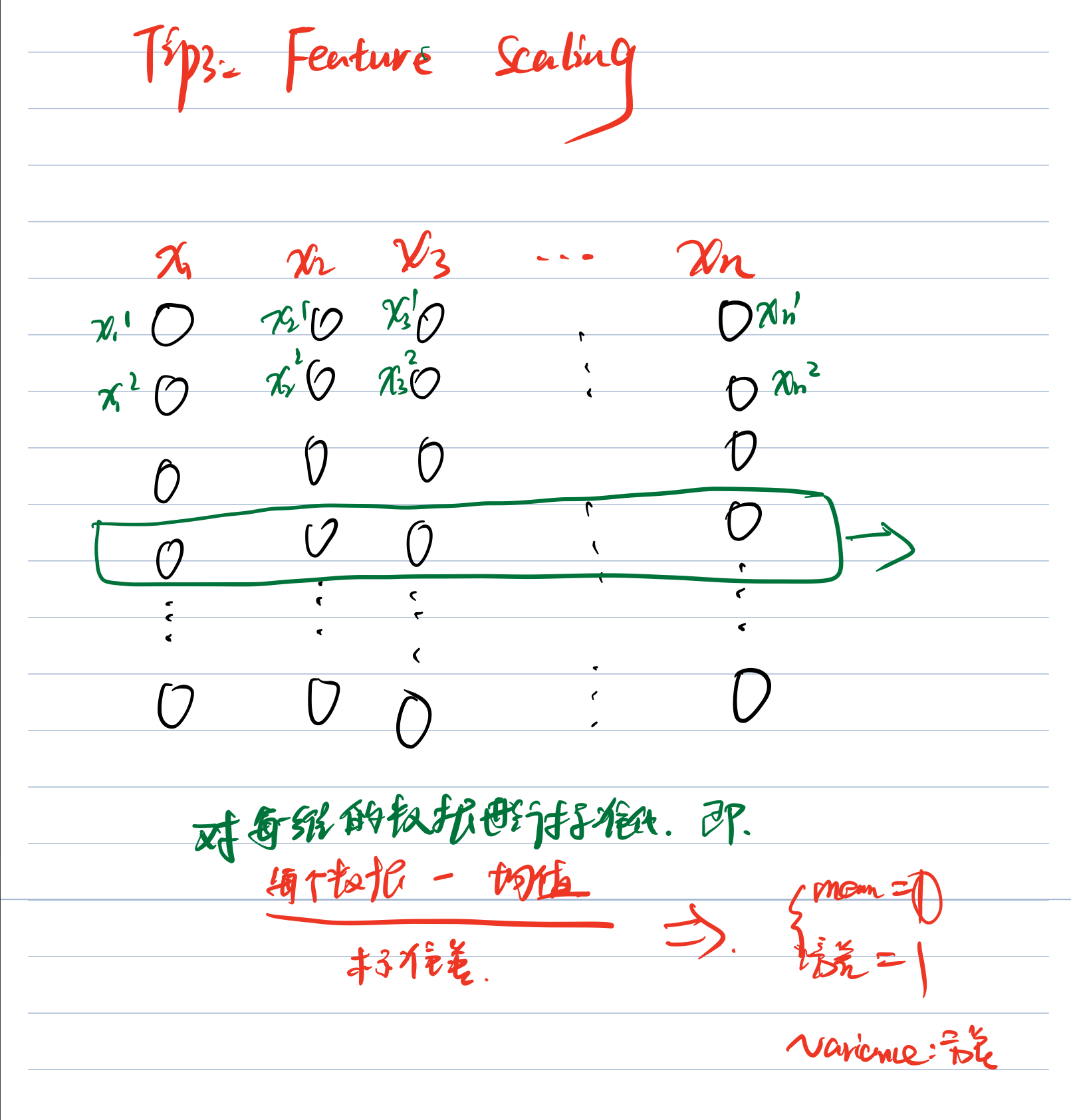
这样做之后这一维数据就会服从均值为0，方差为1的高斯分布。

Code:梯度下降法python实现

背景：

函数（model）：y = w1* x^2 + w2*x + b ,计算出参数 w1 w2 b，给顶的真值是w1_truth = 1.8，w2_truth=2.4，b_truth = 5.6

loss function ：均方误差，公式写出太麻烦，就是y的真实值减去y的预测值的平方和

代码实现

#写一个深度学习的回归案例
#y = w1*x^2 + w2*x + b ,计算出参数 w1 w2 b
import numpy as np
 
#生成数据 
x_data = np.random.rand(10)
w1_truth = 1.8
w2_truth = 2.4
b_truth = 5.6
y_data = np.random.rand(10)
for i in range(10):
    y_data[i] = w1_truth*x_data[i]*x_data[i] + w2_truth*x_data[i] + b_truth
print(y_data.shape)
print(x_data.shape)
 
# 设置参数
w1 = 6
w2 = 4
b = 8
lr = 1
steps = 100000
lr_w1 = 0
lr_w2 = 0
lr_b = 0
for epoch in range(steps):
    w1_grad = 0
    w2_grad = 0
    b_grad = 0
    for i in range(10):
        w1_grad = w1_grad - 2*(y_data[i] - b-w1*x_data[i]*x_data[i]-w2*x_data[i])* (x_data[i]**2)
        w2_grad = w2_grad - 2*(y_data[i] - b-w1*x_data[i]*x_data[i]-w2*x_data[i])* x_data[i]
        b_grad = b_grad - 2*(y_data[i] - b-w1*x_data[i]*x_data[i]-w2*x_data[i])* 1.0
    lr_w1 = lr_w1 + w1_grad**2
    lr_w2 = lr_w2 + w2_grad**2
    lr_b = lr_b + b_grad**2
    # update
    w1 = w1 - lr/np.sqrt(lr_w1) * w1_grad
    w2 = w2 - lr/np.sqrt(lr_w2) * w2_grad
    b  = b  - lr/np.sqrt(lr_b) * b_grad
print("w1= %f,w2 = %f, b= %f" % (w1,w2,b))
#以下是代码的输出结果，可以自己测试一下，完美找到了真实值
# w1= 1.800000,w2 = 2.400000, b= 5.600000

代码中的一些细节

  • 以上代码如果只用一个学习率，收敛会很慢，而且10万个迭代也不会迭代导最终结果，差距还是比较大的，因此代码用的是Adagrad梯度下降法，纯粹手工实现的，可以完美的预测出结果

  • 至于代码中的计算 w1 w2 b 的梯度公式，可以手工推导出来，如下图：

Graph View

Backlinks