入门系列文章: 深度学习入门系列一-梯度下降法 深度学习入门系列一-梯度下降法-② 梯度下降法3 深度学习入门系列4-反向传播BP算法 深度学习入门系列-逻辑回归 深度学习入门系列6-Convolution-Neural-Network-CNN-卷积神经网络 深度学习入门系列7-Tips-For-DeepLearning-全程高能 深度学习入门系列8-Tips-For-DeepLearning-2-全程高能
本文主要讲深度学习中常见的一些但是又理解不透彻的方法原理以及用途,全程高能!
主要有:
- 深度学习流程
- Activation Function(各种)
- 各种梯度下降法
- L1、L2 正则化
- dropout
DeepLearning 流程
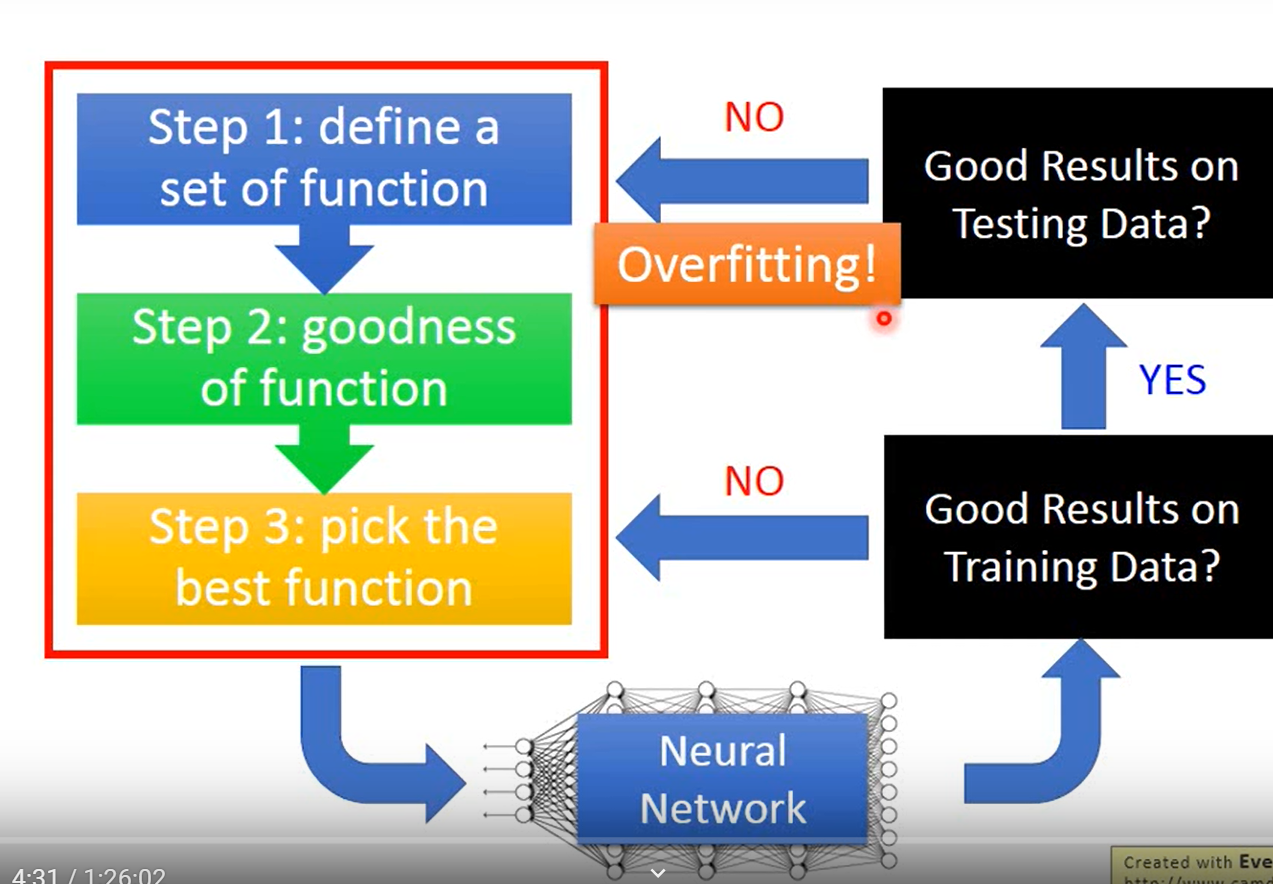
- 首先是之前文章提到过的深度学习的三个步骤,这三个步骤会搭建起一个神经网络;
- 训练神经网络,检测网络对于训练集的效果,此时如果效果很差就要回去调整模型,继续训练,知道得到比较好的结果
- 此时在训练集效果达到了,开始在测试集(验证集)进行测试,如果效果不好就说明过拟合了,需要采取一些措施。
这里要注意,不是说效果一差就是过拟合,要理性分析。
Training set 效果差的原因及其解决
Vanishing Gradient
首先思考一个问题,为什么需要激活函数?
一个普通的全连接网络,如果没有激活函数,那么所有的操作都是乘积、求和,这就是一个线性的网络,表达能力非常差,也不是我们所需要的,因此传统的在每个层后面输出时会加个sigmoid这样的非线性函数。也就是说,激活函数可以使我们的网络编程非线性的。
Sigmoid 函数
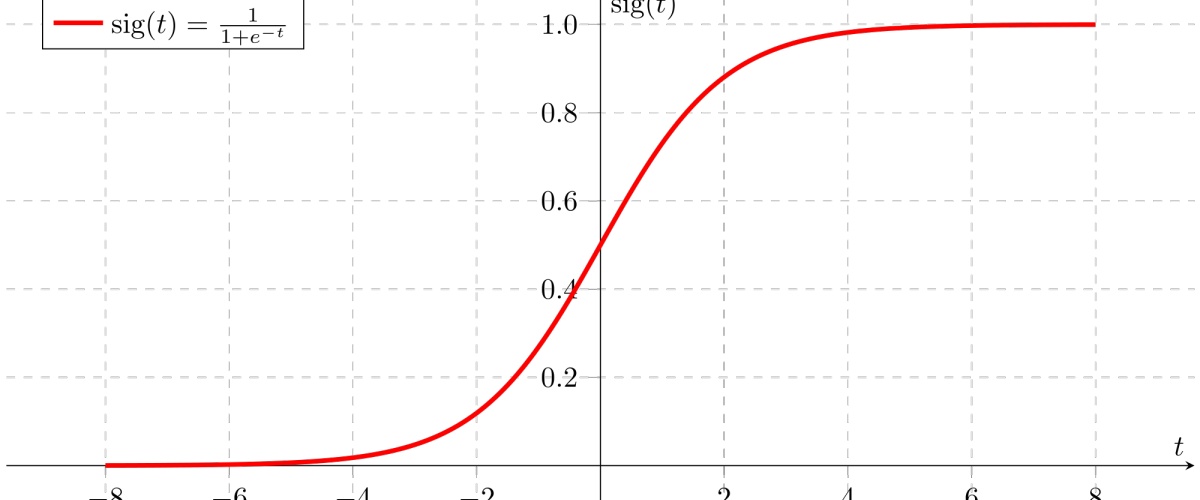
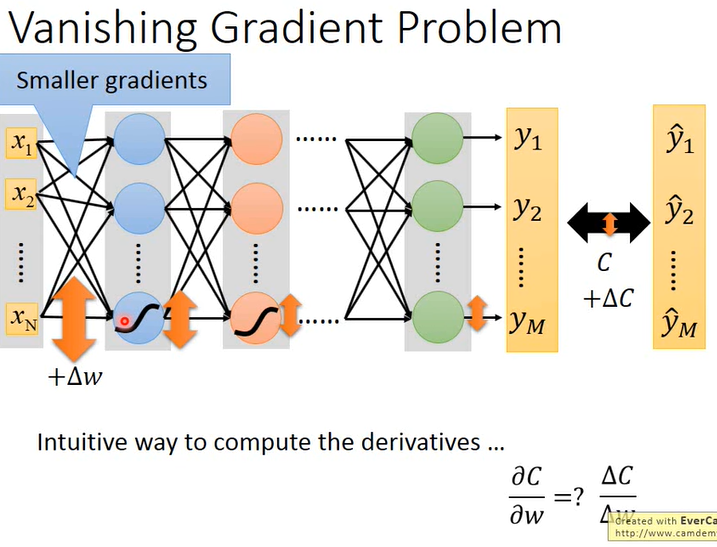
如图所示,所有的输入经过sigmoid会强行压缩到0-1之间,这样会使函数变成非线性的,但是也随之带来了问题:强行将所有之压缩到0-1,随着网络层数的加深,反向传播时靠近输出层的梯度值还比较大,但是输入层附近的层梯度都会很小,梯度从后往前越来越小直到消失,这就是梯度弥散 (gradient Vanish )问题.
- 靠近输出层的参数更新幅度比较快,但是此时靠近输入层的梯度已经很小接近于0,参数基本无更新,也就是还是随机值的状态来更新后面的参数,所以此时后面更新的参数问题就很大!
- 当输入层某个w发生变化就算变化非常大,而sigmoid的值变化幅度确非常的小,因为函数曲线很缓,如下图
ReLu 函数
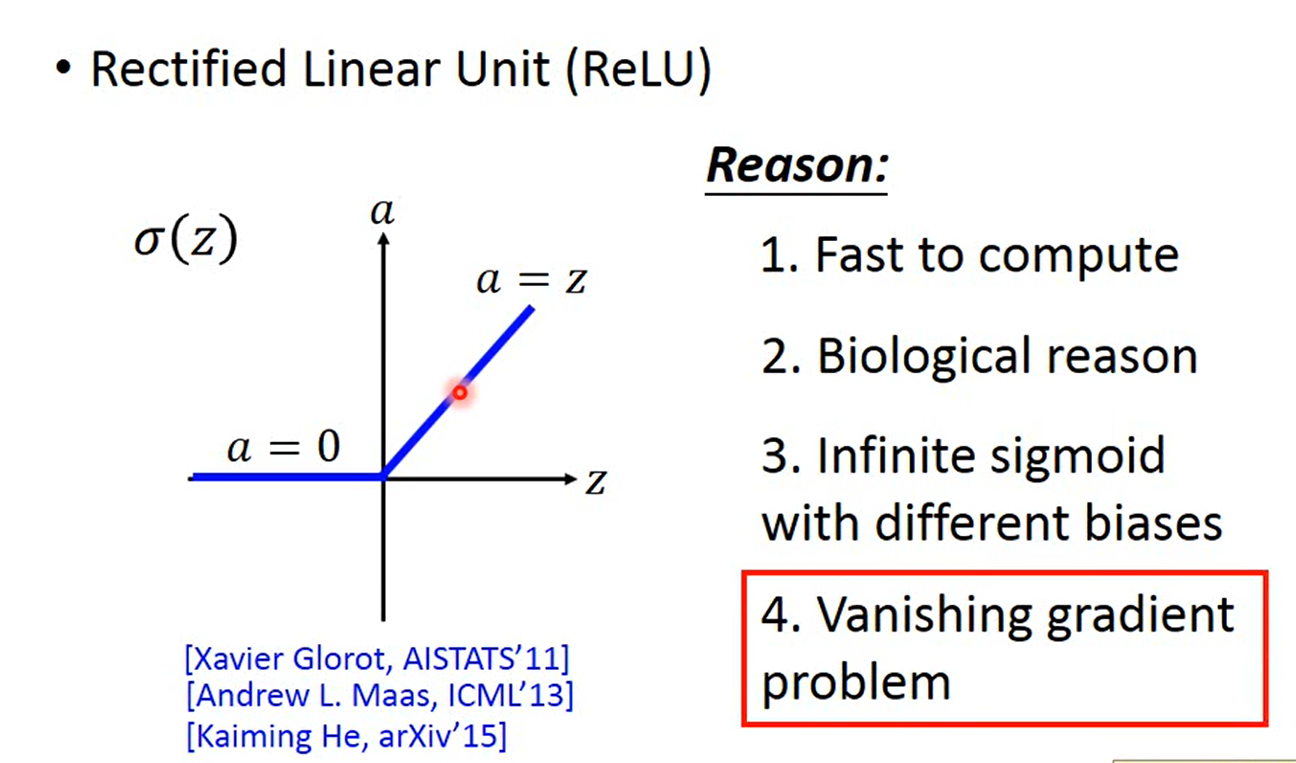
如图所示,输出值a小于0,则 Relu(a) = 0 否则,Relu(a) = a
这个激活函数的出现解决了梯度弥散问题
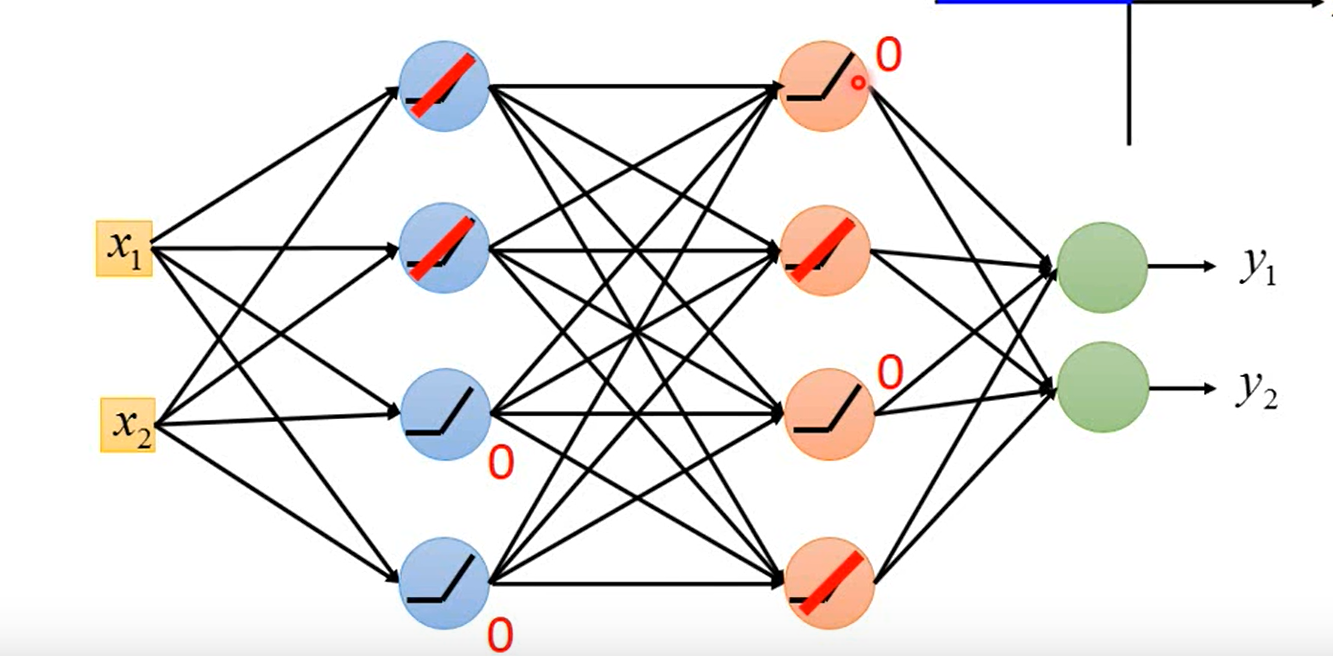
解决方式如图,值为0的神经元可以去掉,整个网络就是一个线性函数了。
这里有一个问题是:0的神经元消除,整个网络就是一个线性函数,这不符合我们要求啊?
可以这样解释,改变了数据输入,神经元的连线发生变化,整个网络依然是非线性的。
着重理解Relu,它的一系列的变体函数就不说了,比较相似
CNN文章提到的Max Pooling 不可导,和这个就很相似了,每次都是取最大值,然后其他的神经元都丢掉,整个网络又是一个细长的线性神经网络。其实是和下面的 Max-out函数比较相似
Max-Out 函数

这个方法是打组思想,Relu就是它的一个个例,这里就不细说了,relu用的多一点。
有个问题:这个每次只取最大的这样有的神经元就不会被train到。因为每次数据不同得到的最大值也会不同,所以所有的weight都会得到更新,都会被train到。
Learning Rate
梯度下降法的时候,会有局学习率问题,所以出现了一些梯度下降法的变体。
Gradient Descent、Adagrad Gradient Descent 、以及 SGD 在之前文章都有讲过,不清楚可以返回看一下。
Adagrad梯度下降法实现了自适应的学习率,但是实际上我们面对的比这个所能解决的问题更加复杂,如下图。
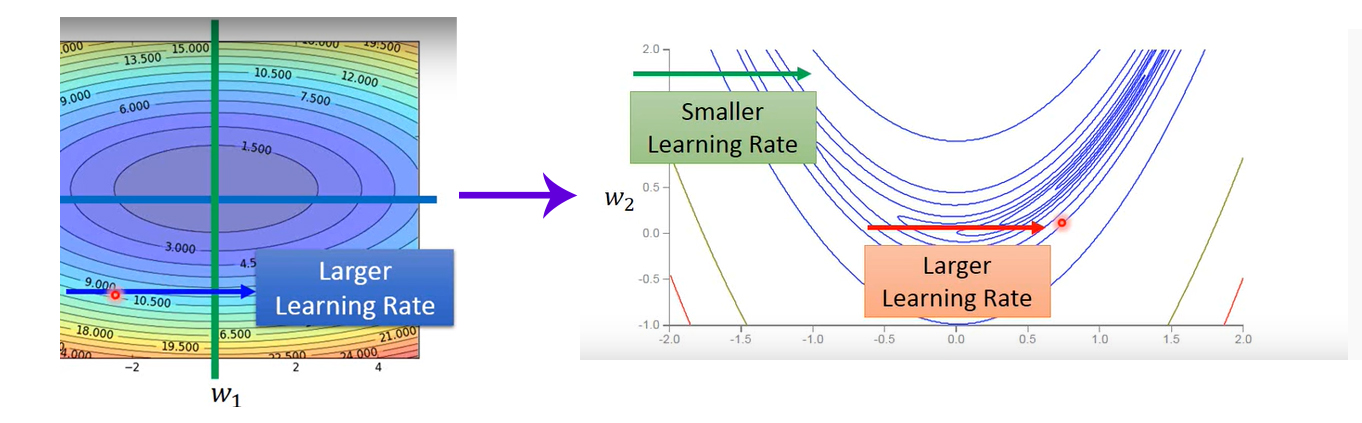
- 左边的在w1方向,从左到右是比较平坦的,所以一个学习率就可以;
- 右边的图同样在w1方向比较缓的地方学习率就应该小点儿,突然陡峭学习率又应该大一点。因此需要更加动态的调整学习率。
Root Mean Square Prop(RMSProp)

与之前的Adagrad方法非常类似,不同的是,这个方法可以控制权重,更偏向于过去的信息还是新的梯度信息,可以通过设置权重值来控制
Local Minimum
Momentum (冲量、惯性)算法
如下图,在求出当前阶段的梯度值后,不只是考虑当前的梯度方向,同时考虑了前一个梯度方向,然后做个加权和得到新的方向。
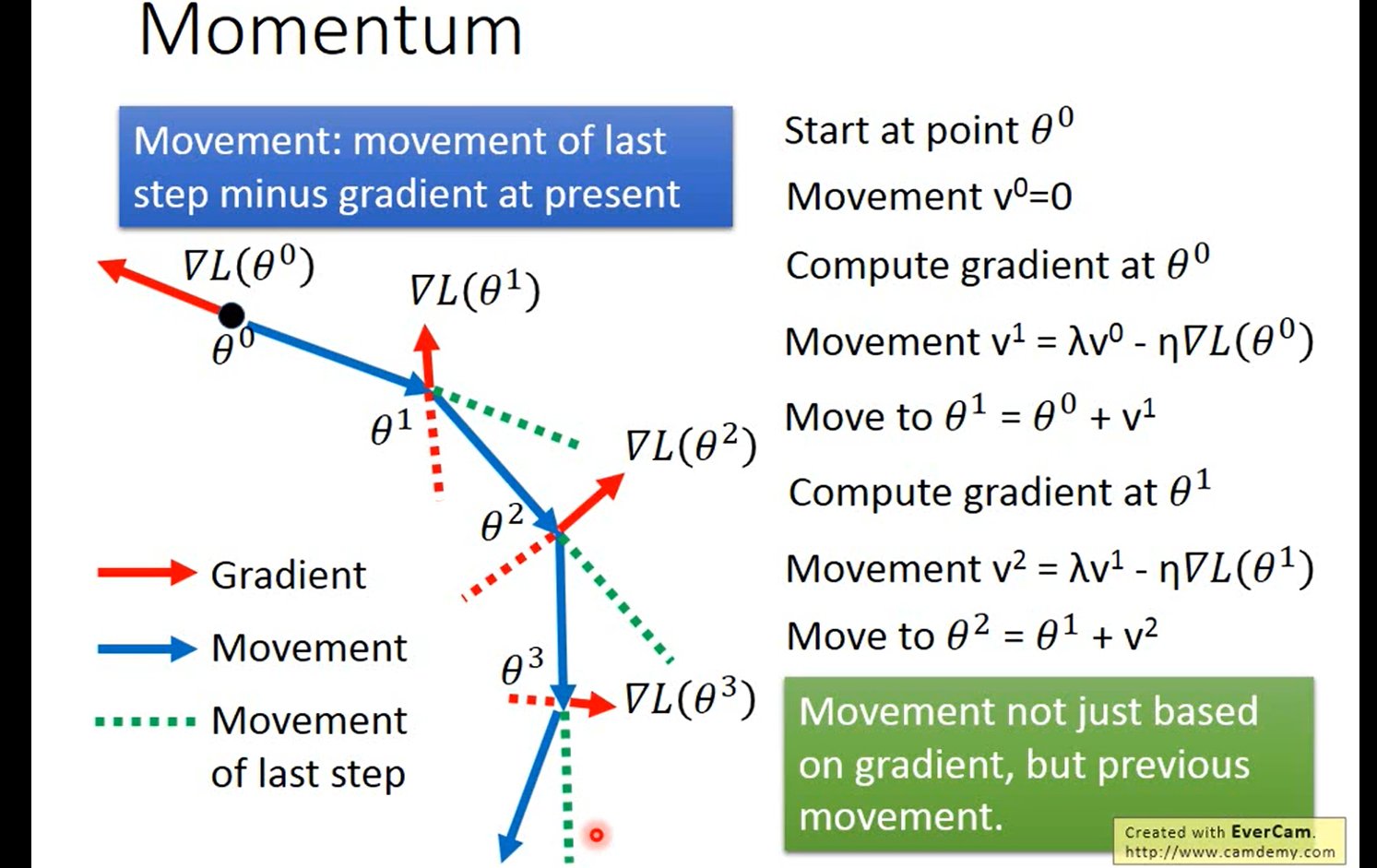
这可以说是根据现实生活中的惯性,会继续向前走一点。
Adam 优化算法
Adam则是 RMSProp、Momentum两个梯度下降算法的集大成者。在深度学习框架中是已经封装好的。这个并未深究,我觉得理解了基础的就可以。
关于测试集效果差,且听下回分解。
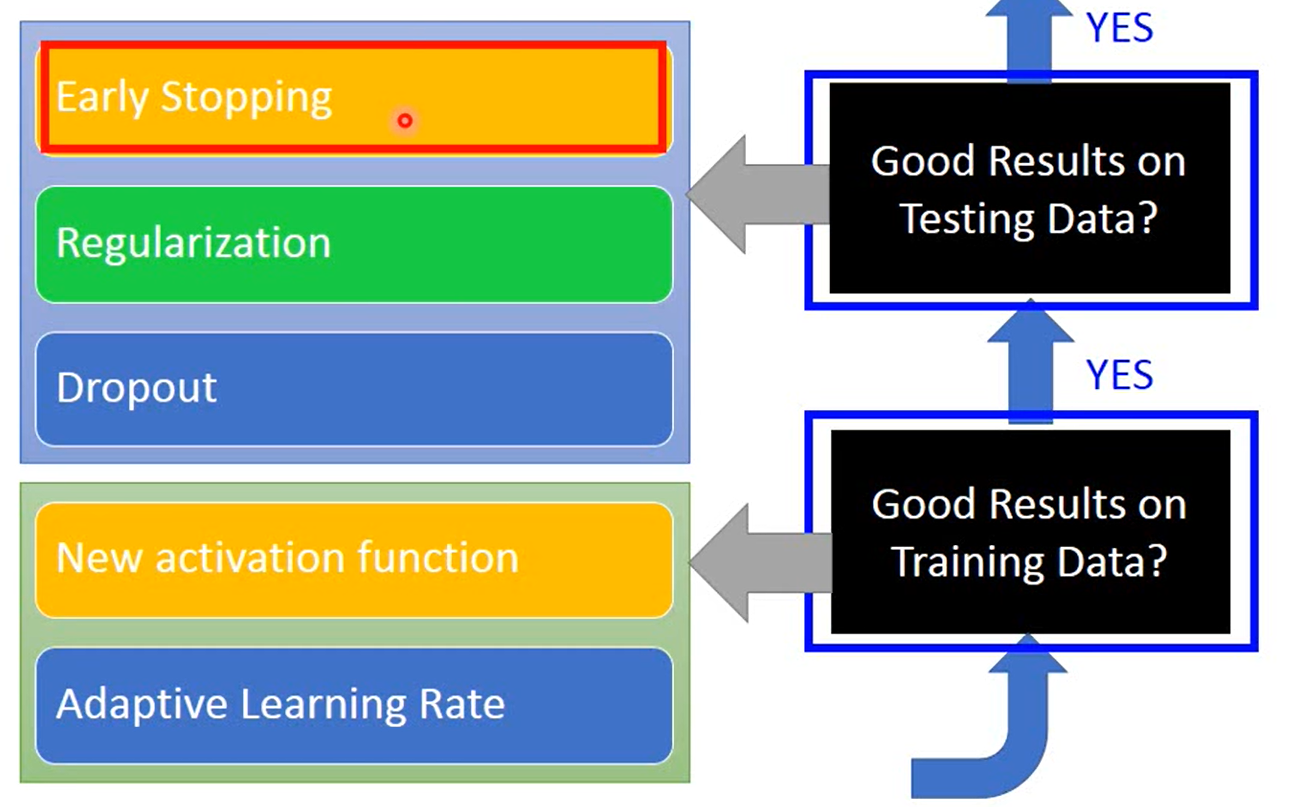
主要讲正则化、Dropout这两块。上图中前两种方法都是比较经典的,不只是深度学习的,而正则化用的多一点,所以主要理解一下正则化; Dropout则是非常具有深度学习风格,所以需要深究。