入门系列文章: 深度学习入门系列一-梯度下降法 深度学习入门系列一-梯度下降法-② 梯度下降法3 深度学习入门系列4-反向传播BP算法 深度学习入门系列-逻辑回归 深度学习入门系列6-Convolution-Neural-Network-CNN-卷积神经网络 深度学习入门系列7-Tips-For-DeepLearning-全程高能 深度学习入门系列8-Tips-For-DeepLearning-2-全程高能
前一篇中文讨论到,在深度学习过程中如果在训练集效果差怎么办,这里接着讨论后半部分,在训练集得到了想要了的效果,但是测试集(验证集,或者是有标签的一些数据)效果并不理想应该怎么办?有如下几种方案、方法可以参考一下:
- Early Stopping
- Regularization
- Dropout
Early Stopping
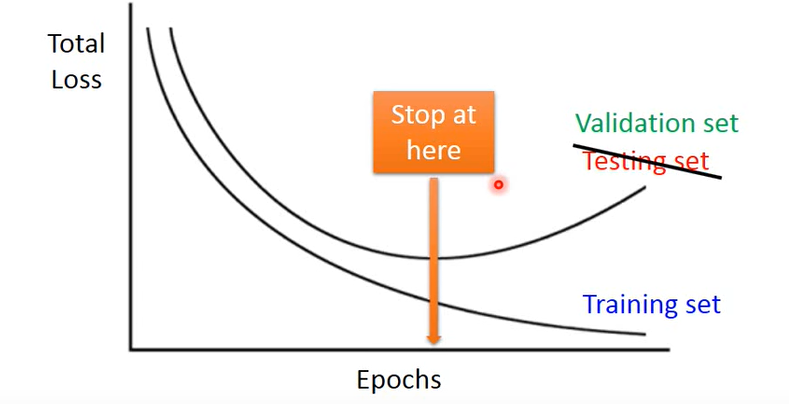
这个方法大致提一下。深度学习中我们有一个假设:训练集和测试集分布是一样的。但是实际上可能并不会如此,我们训练模型应该在验证机loss最低的时候停下来,这就是这个方法的基本思想,具体的可以查阅下 文档。这里我自己主要也是了解一下即可,知道有这么一回事。
Regularization
- 正则化的目的是使得函数更加的平滑,因此正则化一般不对 bias 偏置做;
- 正则化会使得参数变小
- 正则化并不是非常的重要,效果不会非常显著
L2 正则化

首先是右上角L2范数,是w的平方和。
然后是下面的公式推导,L‘是损失函数,L’对某一个w微分,就是后面的结果,然后更新参数公式也很顺理成章,整理到最后就是会在w之前✖一个系数,并且这个系数通常是一个很小的值,整个这个系数接近1,因此每个参数每次更新前会越来越接近0;第一项与第二项最后会实现平衡。
这个手段也成为 Weight Decay,权重衰减
L1 正则化
L1范数是绝对值求和。那么绝对值微分问题就是在真的走到0时直接随便丢一个value比如0当作微分。

L‘对于某一个w的微分就是上图中所推导的,后面的sgn(w)意为:w为正则为1,w为负则为-1.
更新参数时总是在后面减去一项学习率 * 权重 * (1或-1),w为正数时减去一个数,w为负数时加上一个数,总之就是使得参数更加地接近0
Contrast
L1、L2正则化都是使得参数变小,但是略有不同;
- L1每次剪掉固定的值,
- L2则是每次乘以一个固定的值,
如果有一个参数很大,那么用L2正则化更新就比较快;用L1正则化更新依然很慢;
如果有一个参数很小,那么L2正则化更新就很慢;L1正则化 更新会比较快
正则化中的权值衰减,与人的神经网络有异曲同工之妙
Dropout
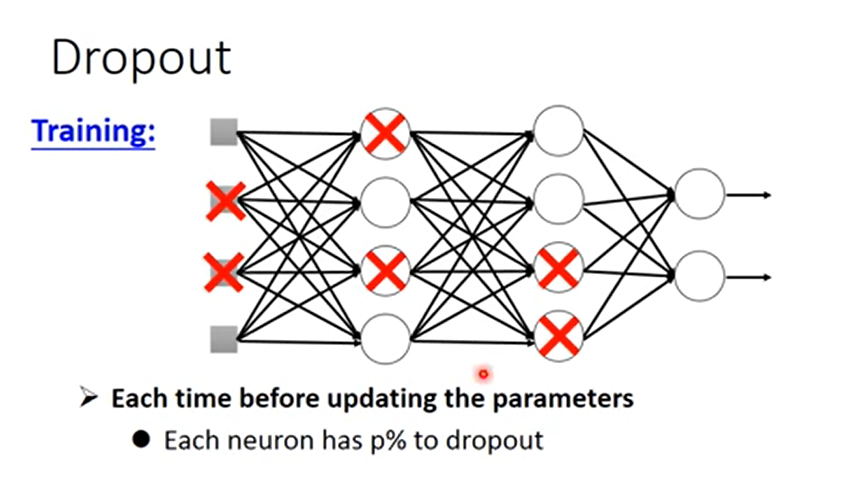
Dropout方法训练流程是这样:
-
设置一个 dropout rate :p%,也就是说在训练时每层会有 p% 的神经元被丢掉;
-
然后每次更新参数都会重新采样丢掉的神经元。
Dropout的测试:
测试期间所有的神经元保留,然后最后丢失率是多少,每个w 都要乘上(1 - 丢失率)。
原理
dropout可以解释为训练了一系列的神经网络,然后最后输出的值取了个平均
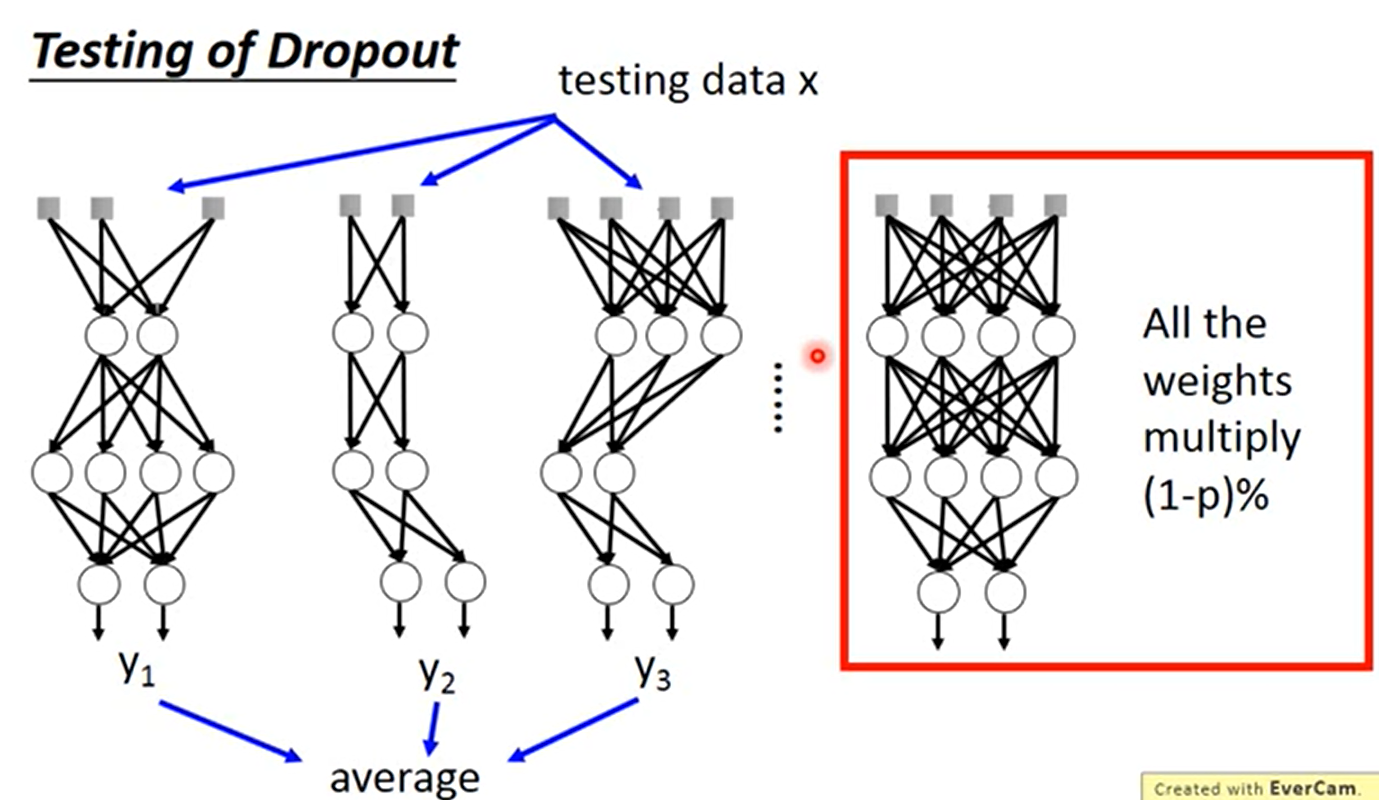
如上图,dropout在所有的weight✖ (1-p%) 就取得了数个神经网络做平均的相近的结果。这也就是这个方法最神奇的地方。
Summary
在深度学习中遇到的问题分为 training data set test set data 效果差
在训练集效果差
梯度弥散
- relu 激活函数
- maxout 激活函数
学习率
- Adagrad
- RMSProp
局部最小化
- Momentum 算法
- Adam
在训练集效果好但是在测试集效果差(过拟合)
- Easy Stopping
- L1、L2正则化
- Dropout