反向传播BP算法

入门系列文章： 深度学习入门系列一-梯度下降法深度学习入门系列一-梯度下降法-② 梯度下降法3 深度学习入门系列4-反向传播BP算法深度学习入门系列-逻辑回归深度学习入门系列6-Convolution-Neural-Network-CNN-卷积神经网络深度学习入门系列7-Tips-For-DeepLearning-全程高能深度学习入门系列8-Tips-For-DeepLearning-2-全程高能

之前讲过机器学习的三个步骤，深度学习Deep Learning非常的类似，可以概括为以下几步：

(设置函数) → 搭建神经网络
(函数的好坏定义) → 设置损失函数
(找出最优函数) → 反向传播更新参数

第一步之前的设置函数，在这里用神经网络来替代了；

在线性回归逻辑回归中可以直接计算梯度，但是深度学习神经网络比较深，不能一下子求出梯度，因此本文主要来探讨一下反向传播 Back Propagation算法。

同时，本文会附上手动搭建神经网络、计算梯度、实现反向传播的代码，纯手写只用到了numpy库！

前置知识

神经网络的反向传播并不需要很高深的数学知识，需要掌握链式求导法则 (Chain Rule)。下面会一步步从数学上求出微分，并且理解这种算法的精妙之处。

案例背景

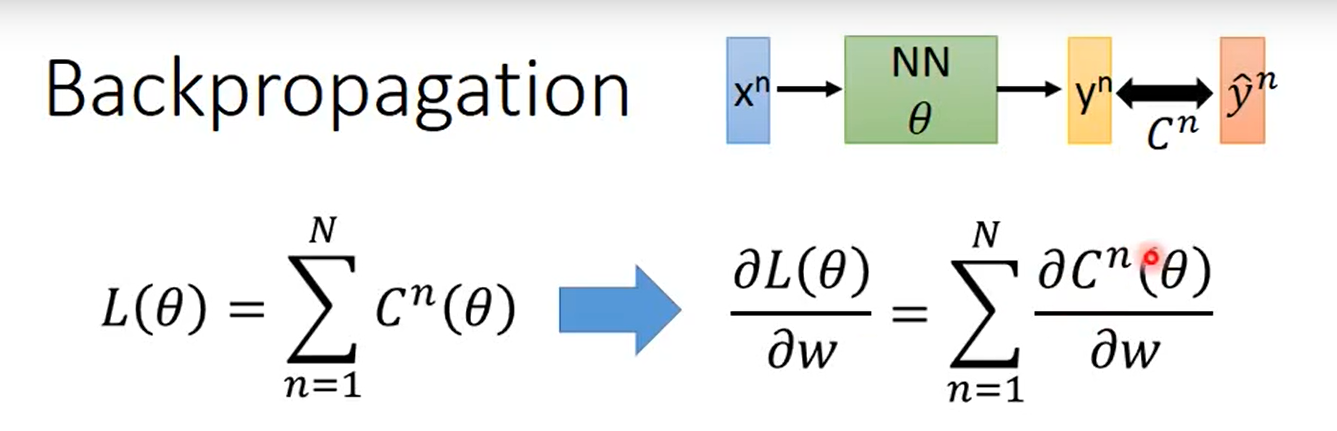
一个有代表性的例子，输入层经过神经网络得到输出值，与真实值之间存在误差，这里用交叉熵作为损失函数，因此在这里，要求梯度也就是求损失函数对于w的偏微分。

层层深入

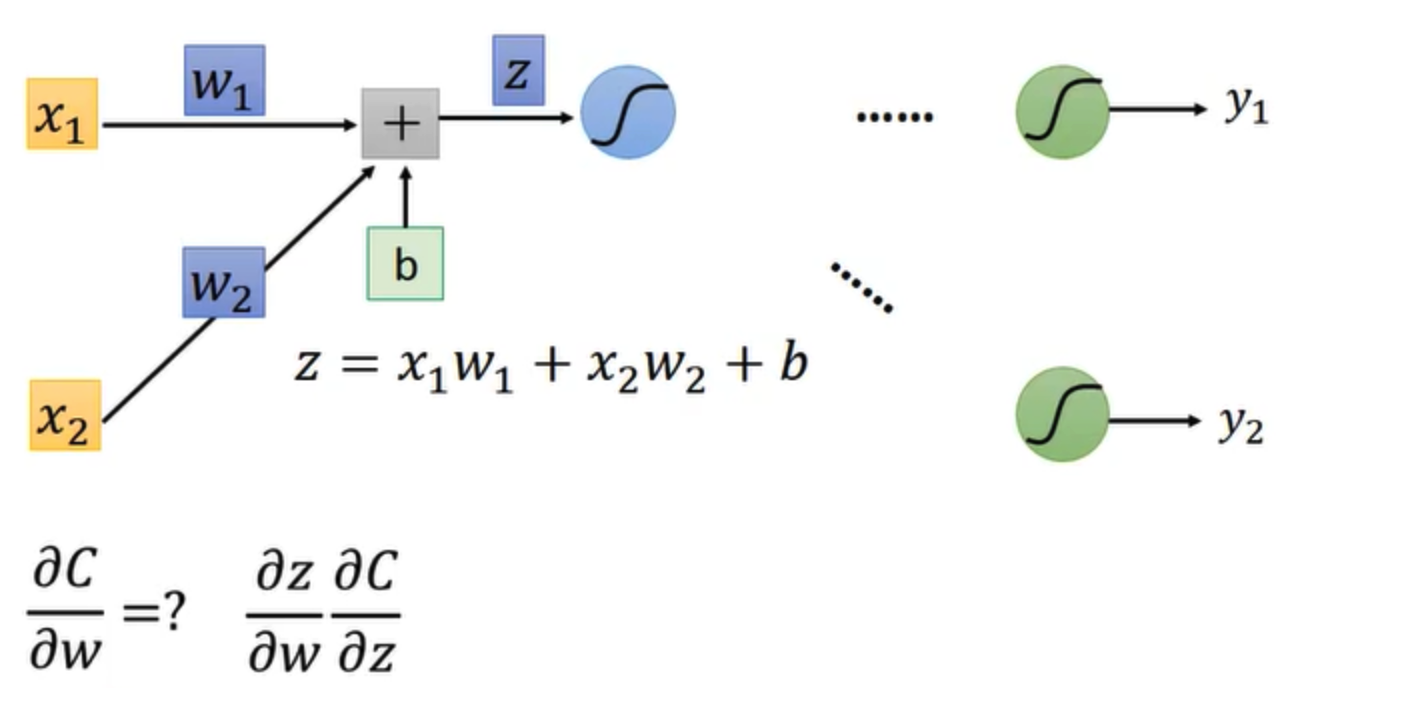
把上面具体的神经网络展开，假设只有两个神经元，这里只对w求微分，b的方式是一样的，所以以w为例。

首先，根据上图的函数以及chain rules，损失函数C对w的偏微分可以拆解为两部分

C 对于 z 的偏导数
z 对于 w 的偏导数

Forward Pass

（先讲第二部分）其中，z 对于 w 的偏导数比较容易，可以很容易的看出来 z 对于 w1 的偏导数就是w之前的输入值，也就是 x1，同理 z 对于 w2 的偏导数就是 x2，下面的图强化一下 z 对于 w 的偏导数

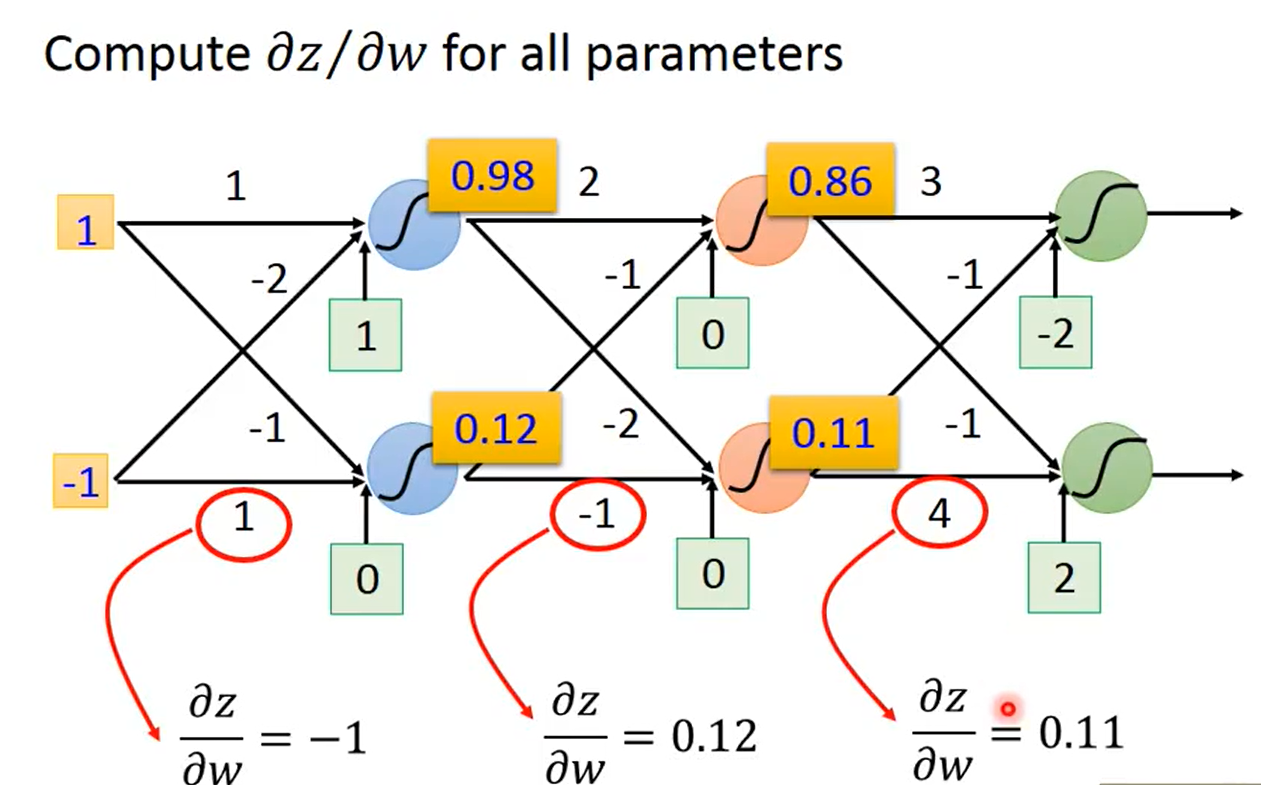
可以观察到z对于每个w的偏导数就是当前权重所之前的输入值，这样比较拗口，英语会比较好理解：

The value of the input connected by the weight .通俗的说就是这条线从哪里出来，出来的那个节点值就是z对于这条线也就是这个w的偏微分。

这里也可以看出，前向传播可以算出每个中间值，也就是计算出了每个梯度的上述第二部分。

Backward Pass

下面看第一部分比较复杂的，也就是 C 对于 z 的偏导数。

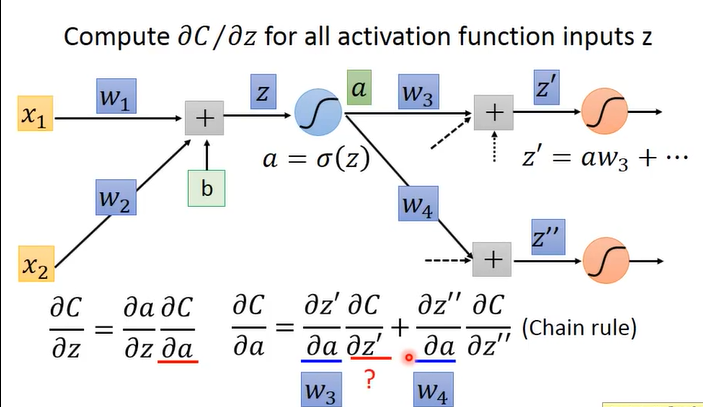
1581523046931

上图中 z 经过 sigmoid 函数得到 a，a 继续传播到下一层，此时 C 对于 z 的偏导数可以转化为上图中的下面公式所写的。在求和的两部分中，同样的各自又都分为两部分，与上述的两部分类似。z’ 对于 a 的偏导数很容易，就直接是 w3 ，相应的 z’‘ 就是 w4.

所以此时问题就转化为 C对于z’ C对于z‘’ 的偏微分，如果这两部分知道那么就可以求出来 C对a的偏微分，同样的C对z的偏微分也就求出来了，也就解决了这部分问题。以下内容是关键：

反求

上图的下面的公式只是把值带入了前一步中的公式，但是可以想象一下，这里面的乘法、加法操作很像是神经网络的前向传播，所以这里就可以想象成一个新的神经网络，只不过是反过来计算的，这时候就会计算出来 C 对于 z 的偏微分。值得注意的是上图中 sigmoid’(z) 是个常数，因为z前向传播时已经计算出来了，所以这里就是计算一个数而已。因此现在到这一步，说明知道后面两项的偏微分可以求出前面的。 此时问题依然是 C对于z’ C对于z‘’ 的偏微分。

大胆假设、细心求证

假设一 (easy)

假设 z‘ z’‘ 之后经过激活函数直接是最终的输出，此时求微分就很简单了，如下图：

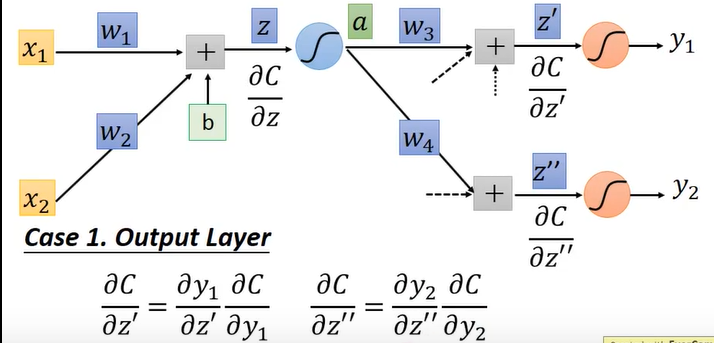
1581524647050

其中，C 对于 y1 的偏微分就是损失函数的偏微分，y1 对于 z’ 的偏微分就是根据激活函数（上图最后的橙色圆圈）求出微分很容易，z‘’ 同理。

在此种假设下，此时已经得出了 C 对于 z‘、 C 对于 z’‘ 的偏微分，回溯到前一个步骤，就求出了 C对于z的偏导，在往前回到最初步，发现此时已经求出了两个需要的条件，此时就可以算出 C 对于 w1 ，C 对于 w2 的偏微分。

也就是说，忙活到现在，也就只是算出来了第一个神经元的两条线(2个w)的梯度！

假设二 (Normal)

假设 z‘ z’‘ 之后依然有很多层，如下图：

)

由反求部分我们已经知道想要求 C对于 z’（or z‘’）的偏导数，需要知道后面 C 对于 Za 及 Zb 的偏导数，所以需求会一直往后寻找，递归这个过程，知道到达输出层，然后一层层往前就会求出来最初始的梯度，如下图：

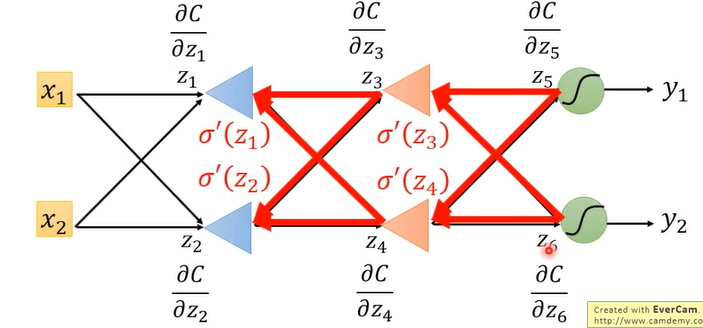
至此，如果理解了这些，就已经理解了反向传播的原理了。

Conclusion & Question

BP算法总结

Back Propagation 算法分为两部分

前向传播求出 z 对于 w 的偏导数
反向传播求出 C 对于 z 的偏导数
两个值相乘就是梯度

思考

从前到后的传播直接计算每个参数的梯度为什么比BP算法差?

前向传播计算梯度

从前到后直接传播计算梯度，第一层的w需要知道后面所有的层的梯度，此时会进行一趟计算；2-end；

继续求第二层w 的梯度，需要知道后面所有层的梯度，也就是 3 - end；最后加起来就是：

end - 2 + end - 3 + end - 4 + … + end-0,z明显计算量不小！

反向传播计算梯度

从最后一层开始计算，先计算出最后一层梯度，可以直接计算出来，这样每次往前计算不用再一直累加，因此计算量小很多。所以说BP算法刚好就是利用了原来的网络和参数而且可以用和前向传播相同的计算量计算出所有w的梯度。这就是BP算法的精妙之处！

代码实现

在这里手动搭建了一个神经网络，暂时没有考虑b，因为只是用来加深理解，又一个输入层，两个隐藏层，一个输出层，每层四个神经元。所有参数都是手动计算梯度。

根据以上分析的反向传播算法可以总结出以下几步：

前向传播一遍计算出所有节点的值
反向传播一遍计算出所有结点的偏微分
做乘法求出所有的梯度进行更新

import numpy as np
#Generate data
# Forward Node
x_F = np.random.rand(4)
y_F = np.random.rand(4)
z_F = np.random.rand(4)
p_F = np.random.rand(4)
 
#weight
x_y_w = np.random.rand(4,4)
y_z_w = np.random.rand(4,4)
z_p_w = np.random.rand(4,4)
#backward node
x_B = np.random.rand(4)
y_B = np.random.rand(4)
z_B = np.random.rand(4)
p_B = np.random.rand(4)
 
#TARGET
target = np.array([0.5,0.7,0.3,0.1])
#loss
def SquareErrorLoss(output, target):
    loss = 0
    for i in range(len(output)):
        loss = loss + (output[i] - target[i])**2
    loss = loss
    return loss
 
# Graident
lr = 0.0000001
for epoch in range(500000):
    # forward0
    y_F = np.matmul(x_F, x_y_w)
    z_F = np.matmul(y_F, y_z_w)
    p_F = np.matmul(z_F, z_p_w)  # 得到输出
    loss_end = SquareErrorLoss(p_F, target)
    # backward
    p_B = 2*p_F  # end grad
    z_B = np.matmul(p_B, z_p_w.T)
    y_B = np.matmul(z_B, y_z_w.T)
    # print(z_F[0])
 
    # grad
    z_p_w_grad = [np.dot(z_F[0], p_B),
                  np.dot(z_F[1], p_B),
                  np.dot(z_F[2], p_B),
                  np.dot(z_F[3], p_B)]  # 4*4
    y_z_w_grad = [np.dot(y_F[0], z_B),
                  np.dot(y_F[1], z_B),
                  np.dot(y_F[2], z_B),
                  np.dot(y_F[3], z_B)]  # 4*4
    x_y_w_grad = [np.dot(x_F[0], y_B),
                  np.dot(x_F[1], y_B),
                  np.dot(x_F[2], y_B),
                  np.dot(x_F[3], y_B)]  # 4*4
    # update
    x_y_w = x_y_w - lr * np.array(x_y_w_grad)
    y_z_w = y_z_w - lr * np.array(y_z_w_grad)
    z_p_w = z_p_w - lr * np.array(z_p_w_grad)
 
    if epoch % 5000 == 0:
        print("当前loss值为")
        print(loss_end)
        print(p_F)
 
#截取输出片段打印
当前loss值为
165.06777280622663
[8.38287281 5.70538503 7.00228248 5.84052431]
当前loss值为
133.11940656598998
[7.56299701 5.15781875 6.33931068 5.28536964]
当前loss值为
109.77775387801975
[6.89894847 4.7147705  5.8028157  4.83622736]
当前loss值为
92.14372363473903
[6.34836332 4.34779557 5.35839007 4.4642465 ]
当前loss值为
78.45934876430728
[5.88318774 4.03806177 4.98325151 4.1503256 ]
当前loss值为
67.60388807433274
[5.48405883 3.77257388 4.66167746 3.88128352]
当前loss值为
58.833090378271265
[5.13715314 3.54205652 4.38244476 3.64771203]
当前loss值为
51.6356735906825
[4.83232077 3.3397007  4.13731374 3.44270456]
... ... ... ... ... ... ... ... ... ... ... ...
当前loss值为
0.34148441938663887
[0.38019982 0.42063884 0.60690939 0.49356868]
当前loss值为
0.33762403308295663
[0.37029135 0.41401346 0.59891746 0.48685882]
当前loss值为
0.3343170568629769
[0.36058041 0.40751086 0.5910724  0.48027121]
当前loss值为
0.3315343883568477
[0.3510625  0.40112821 0.58337076 0.47380298]
当前loss值为
0.3292483287899748
[0.3417333  0.39486274 0.57580922 0.46745137]

以上代码可以看出，loss值不断不断的下降，并且最终趋于稳定，可以说明由之前的推导总结出的方法思路并无问题！

Quartz 4

Explorer