入门系列文章: 深度学习入门系列一-梯度下降法 深度学习入门系列一-梯度下降法-② 梯度下降法3 深度学习入门系列4-反向传播BP算法 深度学习入门系列-逻辑回归 深度学习入门系列6-Convolution-Neural-Network-CNN-卷积神经网络 深度学习入门系列7-Tips-For-DeepLearning-全程高能 深度学习入门系列8-Tips-For-DeepLearning-2-全程高能
逻辑回归,是用于处理因变量为分类变量的回归问题,比如二分类问题,其实是一种分类算法。本文主要对比逻辑回归回归与线性回归的处理过程并探讨其中一些公式、细节。
逻辑回归&线性回归

如上图所示,
- step1确定函数时,逻辑回归函数输出的是个概率值,线性回归输出的可以是任何一个数
- step2确定损失函数,逻辑回归用的交叉熵,线性回归则是均方误差
- step3比较神奇,两个损失函数长得差别很大,但是算到最后更新参数公式竟然是一样的!(后面有推导)
Cross Entropy
背景,一系列函数设置:

设计损失函数:这里有一个假设, x1 x2 …xN 属于 C1 类,真值为1,其余为0

**这里的之所以要取对数,是因为拆开之后求微分比较容易。**蓝色线画的,即是交叉熵,也就是表格中step2的C函数。
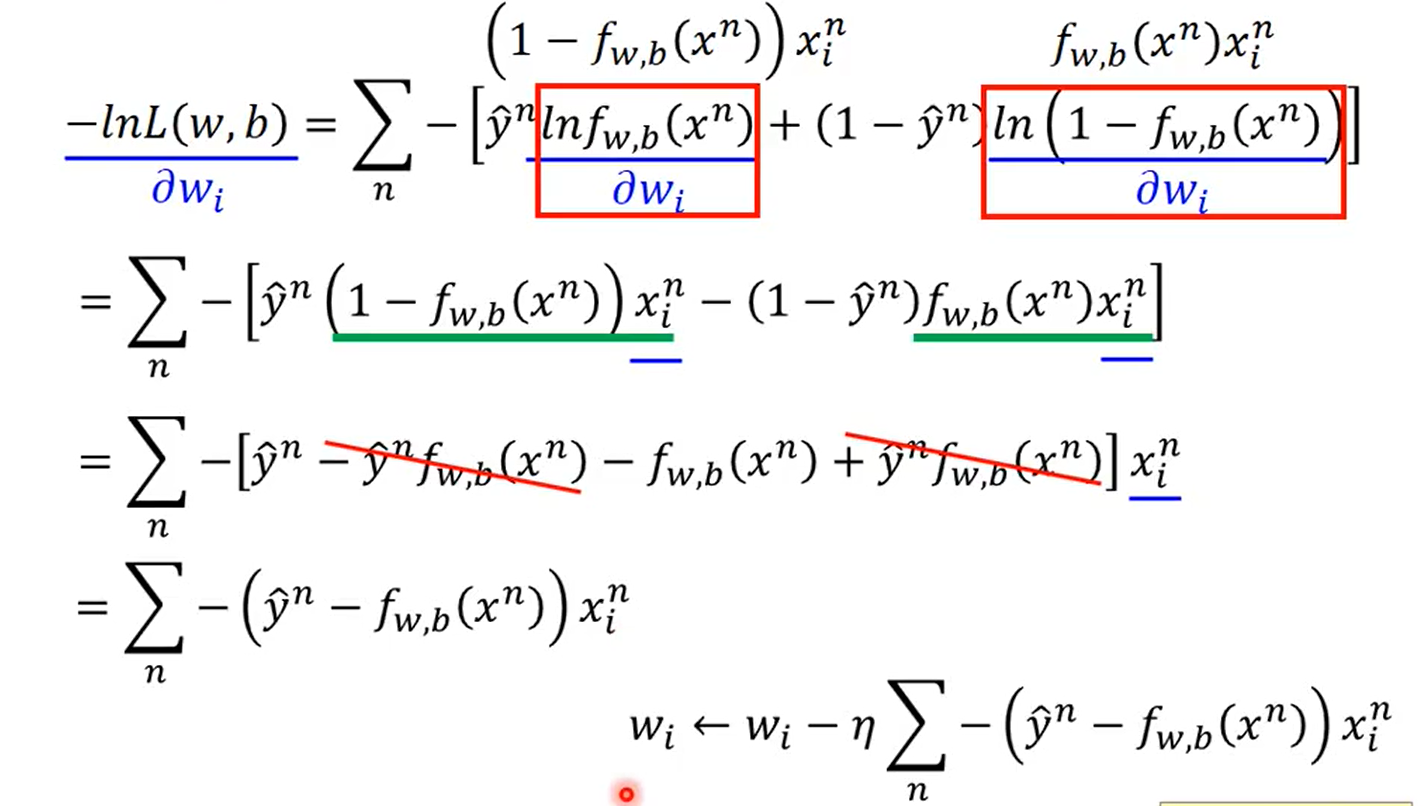
上述函数对w求偏微分之后,也就是求出了梯度,(过程可以自己算一下,挺简单的),就得到了下面的公式,此时更新参数就和线性回归相同也推出来了。
交叉熵和均方误差
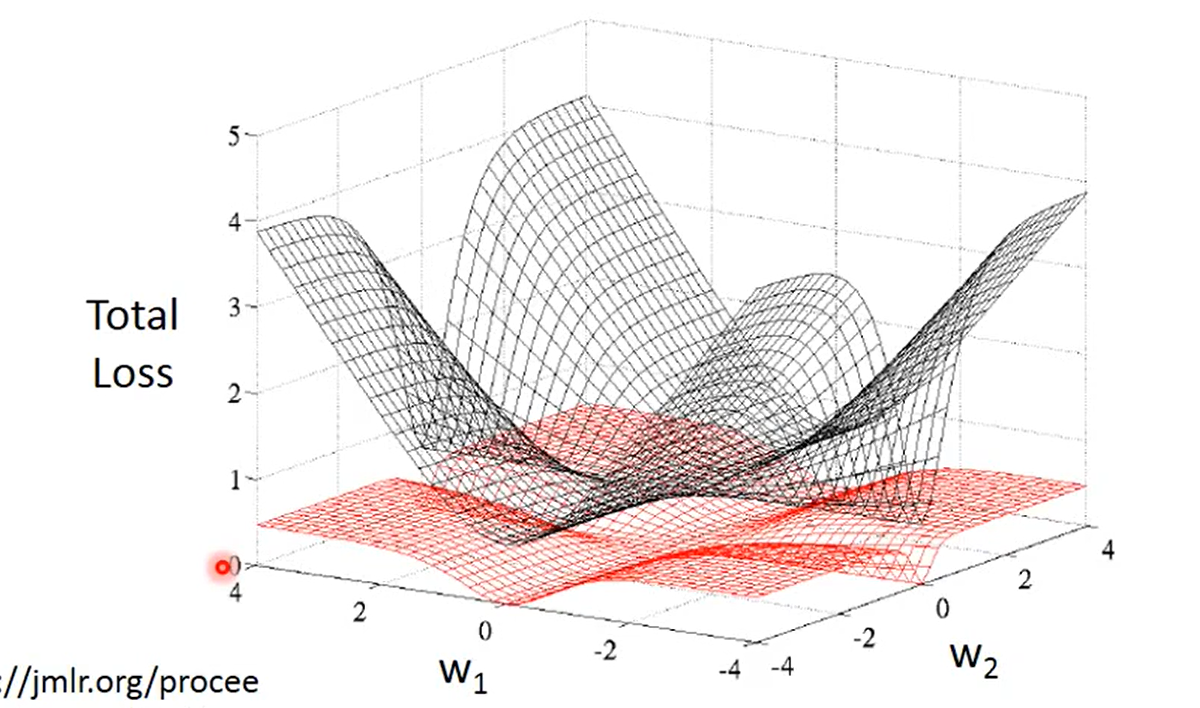
图中黑色曲面的代表交叉熵,红色的曲面代表均方误差,这幅图表达了参数的变化对于整个loss值的影响大小
- 对于Cross Entropy,越边缘的点梯度越大,此时更新参数会比较快
- 对于 Square Error,边缘的点梯度并不大,而接近最小值的点梯度也比较小
Conclusion
由上面的对比可知:逻辑回归如果用均方误差,会导致更新参数非常慢,而直接提高学习率也并不是一个好的选择,因为真正靠近真值时,梯度本来就比较小,较大的学习率此时也并不合理,因此一般来说,逻辑回归(也就是分类问题)可以采用交叉熵作为损失函数。
2020/6/8更新
说实话看以上的确实是一头雾水,可能看完还是不知道什么是逻辑回归,因为上述文章只是说到逻辑回归常用于二分类问题,这里做一些补充、再学习。
白话来说,二分类网络最后一层使用sigmoid函数就是逻辑回归方法,具体原因是:
鉴于要写的东西比较多,决定 新写一篇文章。