入门系列文章: 深度学习入门系列一-梯度下降法 深度学习入门系列一-梯度下降法-② 梯度下降法3 深度学习入门系列4-反向传播BP算法 深度学习入门系列-逻辑回归 深度学习入门系列6-Convolution-Neural-Network-CNN-卷积神经网络 深度学习入门系列7-Tips-For-DeepLearning-全程高能 深度学习入门系列8-Tips-For-DeepLearning-2-全程高能
Gradient Descent 前面的文章讲了基本的流程,可以知道基本的梯度下降法更新参数流程是 w_new = w_origin - のL/のw, 这里为什么是负号呢?为甚要乘以梯度方向呢?这一切要从泰勒级数说起。
Taylor Series
假设函数 h(x) 在 x = x0 处无限可导,那么h(x)可以展开成如下:其中,x很接近x0时,后面的高次项边都可以忽略,因此约等于前两项。
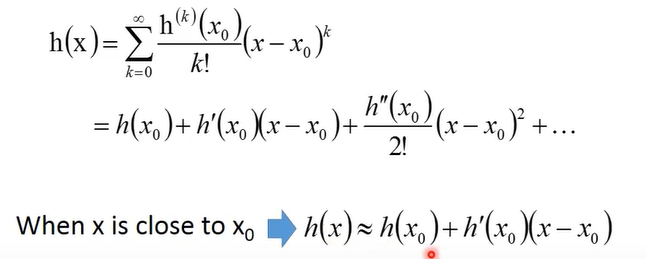
上图是泰勒级数在只有一个变量时的展开式,同样多个变量也可以展开:
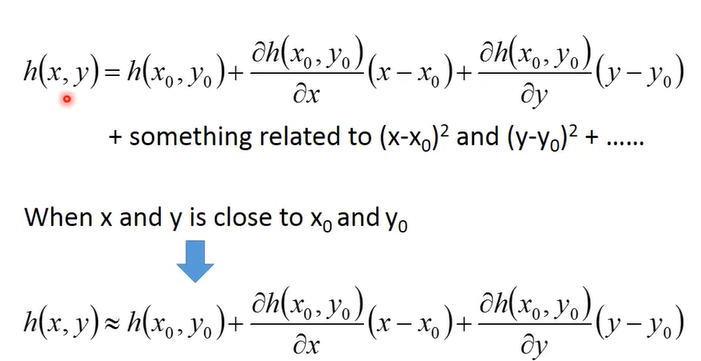
Based Taylor Series
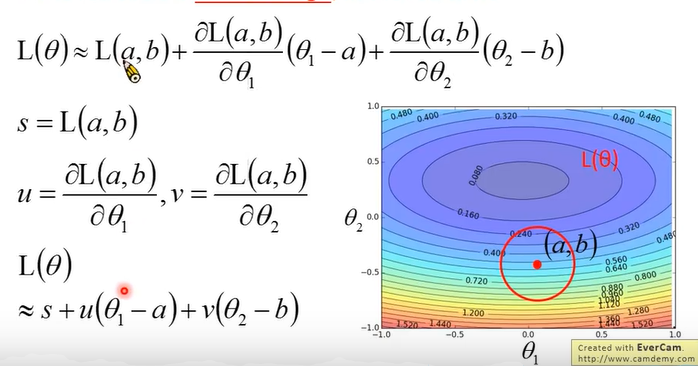
如图,在点(a,b)处取一个足够小的圆,此时损失函数 L(θ) 便可以根据泰勒公式在(a,b)处展开,其中 s,u,v, 三项均为常数。u是L在θ1方向的偏导数,v是L在θ2方向的偏导数。
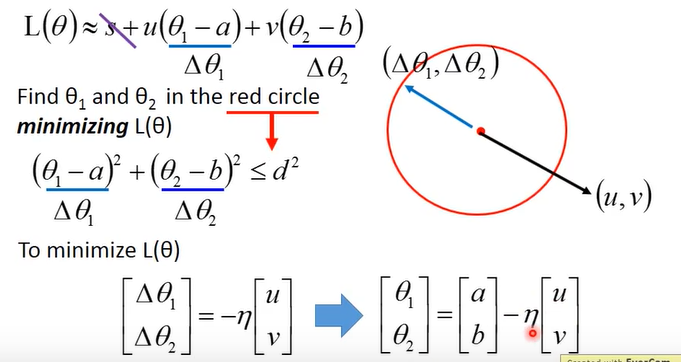
此时要最小化L,把上图公式中 **θ 1 - a **用▲θ1表示,**θ 2 - b **用▲θ2表示,s与θ无关因此可以忽略,公式L 看起来就比较简单了,可以看成是 vector(u, v) 与 vector(▲θ1, ▲θ2) 的内积,则当(▲θ1, ▲θ2)处于圆上(长度最大),方向相反(cos = -1)时内积最小,因此可以得到图中最下面的推导公式,乘以 -n 表示的是比例,使得(▲θ1, ▲θ2)位于圆上,负号则是与(u, v) 方向相反。将(▲θ1, ▲θ2)换算之后便会得出通常的更新参数的公式,因此得出了文章最初的w_new = w_origin - n*のL/のw,因此梯度方向下降最快,要乘以负的学习率。
至此梯度下降法的来源也都已清楚!