牛顿法一般有两个用途:方程求根;最优化。
求根问题
对于高次方程,求根公式要么没有要么就很复杂,此时可以用牛顿法来求解。首先根据泰勒公式,把f(x)在x0出展开到一阶(随机取一个x0求f(x)):
令f(x) = 0得:
由于f(x)用泰勒公式展开到一阶,严格意义上展开式并不相等,只是可以说f(x_1)比f(x_0)更接近0 而已,由此迭代便自然而然了:
通过迭代,必然可以在f(x*) = 0 ,x=x*时收敛。也就是求出了根。
把上面得泰勒公式展开求解迭代过程在几何表示如下图:
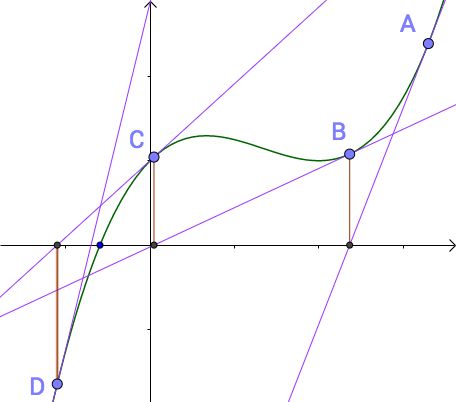
这也是牛顿法的基本原理。
优化问题
前置知识
海塞矩阵:是一个由多变量实值函数的所有二阶偏导数组成的方块矩阵。
使用下标记号表示为:
泰勒展开与海塞矩阵:

流程
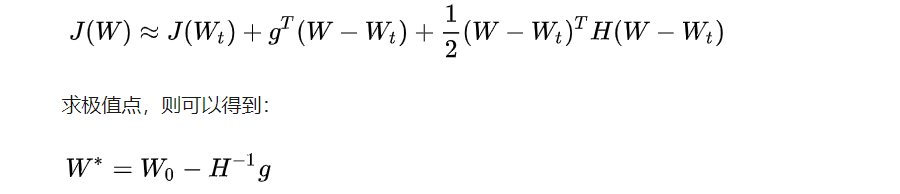
这就是牛顿法更新的公式。此时下降最快的方向就是 海塞矩阵逆矩阵 * 梯度
思考梯度下降法与牛顿法
收敛情况
由求根迭代可以看出,牛顿法显然收敛速度比较快。
- 牛顿法采用二阶海塞矩阵逆矩阵求解
- 梯度下降法采用梯度求解
通俗来说,二阶比一阶收敛更快,因为采用二阶逆矩阵求解,不仅考虑了梯度,也考虑了下一步的梯度,看得更远,所以收敛更快。(来自知乎)
缺陷
牛顿法既然比梯度下降法收敛快,那么为什么在深度学习中并未广泛应用,而是梯度下降法用的更多?原因大致如下:
- 海塞矩阵难以求解,矩阵运算复杂度过高;
- 我认为比较可接受得原因是牛顿法不具有普适性, 用自己得应用范围,而深度学习数据量大且复杂,则更应该采用普适性方法