之前文章讲到过用梯度下降法来更新参数。深度学习反向传播,根据误差调整参数,那么深度学习的error到底来自哪里?这个是比较必要的,可以给我们提高自己的模型提供方案。
这个李宏毅老师讲的很清楚,有需要可以学习一下,附上链接:https://www.bilibili.com/video/av48285039?p=8
Error来源概述
深度学习种Error 来源于两方面:
- bias 偏置
- variance 方差
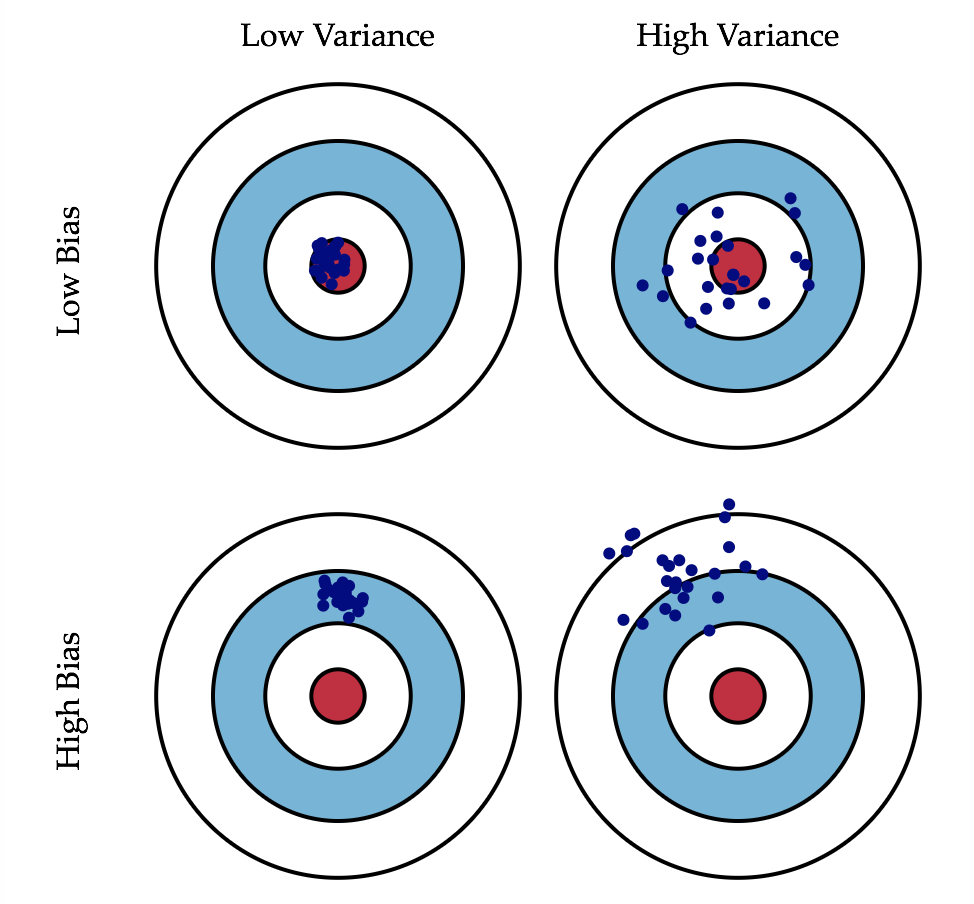
Variance
直观上,方差可以了解为散布的分散程度。上图可以明显的看出比较高的方差,点的散布很分散,比较低的方差则比较紧凑。方差可以用来形容模型的稳定性。一般来说,
比较简单的模型,方差较小,分布比较紧密;比较复杂的模型,方差比较大,分布比较分散
可以如下解释:
- 比较简单的模型,比如 f(x) = c,受数据的影响为0,因此所有值相同,方差为0,分布都在一起
- 比价复杂的模型,比如五次方方程,受到数据的影响会比较大,取到的值很多,因此每次的预测值可能相差很远,此时方差就比较大了
Bias
将所有预测出来的函数求出期望值得到的函数距离真实函数依然会有一段距离,这就是bias,如下图所示,
红线表示100个预测出来的函数,蓝线表示这100个函数的平均,黑线表示真实函数
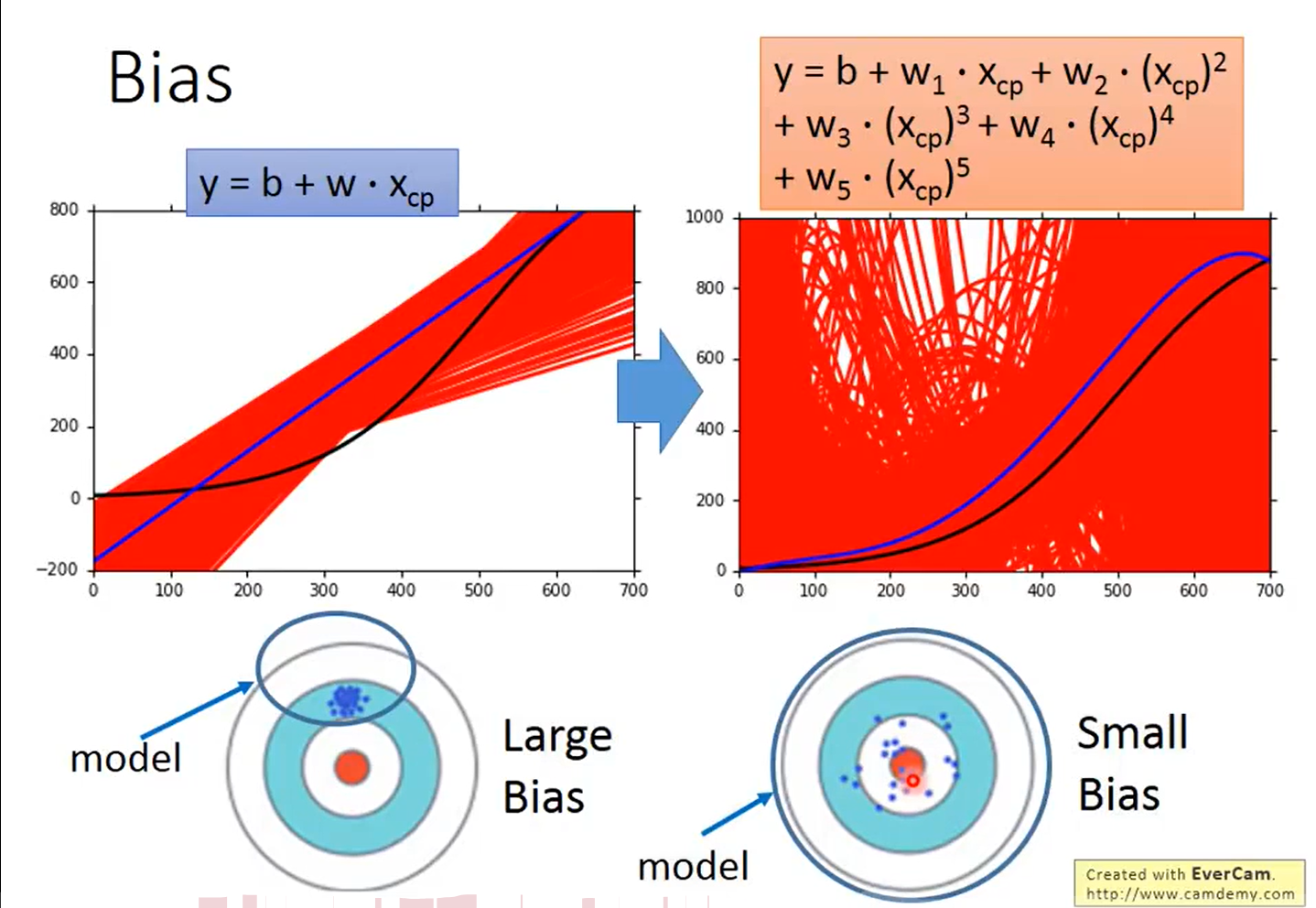
可以看出,简单的模型bias比较大,而复杂的模型bias比较小
可以解释为,上图的底部,我们所设计模型的复杂程度其实也就决定了函数所能表达的范围,过于简单的函数所包含的范围可能根本没有包含到真值,因此bias比较大;而比较复杂的函数范围比较大,包含到了真值,因此bias会比较小。
比较
| 模型复杂程度 | 方差 Variance(精确性) | 偏置Bias(准确性) |
|---|---|---|
| Simple Model | 较小 | 较大 |
| Complex Model | 较大 | 较小 |
总结与改进
了解了误差的来源,那么如何判断自己的模型是什么问题呢?
-
如果模型无法适应训练数据,也就是说在训练集上误差比较大,此时就是 bias 比较大,此时处于**欠拟合状态,(underfitting)**也就是模型过于简单,此时改进:
- 载入更多的特征
- 创建更复杂的模型
- 注意,此时收集数据集增加数据集并起不到作用
-
如果模型在训练集表现得很好,但是在测试集表现得很差,此时就是Variance比较大,也就是**过拟合(overfitting)**了,此时改进:
- 增加数据集,对于过拟合是一个很好的解决办法,如果采集不到更多的数据,则可以利用现有的数据去生成更多新的数据
- Regularization 正则化 ,正则化的效果是使得到的曲线更加的平滑,如下图
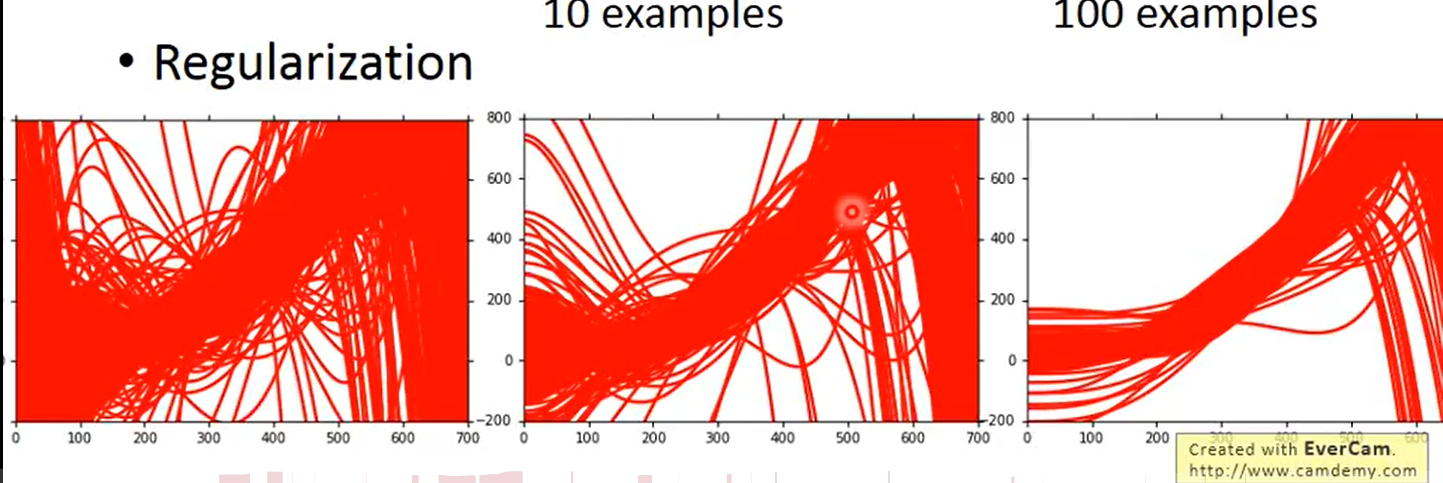
Regularization
以线性回归为例,在损失函数的最后加上一项 参数 wi的平方和,这就会要求w越小越好,起到限制作用

-
此时函数会比较平滑,平滑即对输入不会非常敏感,至于为什么会比较平滑,可以看上图下面部分,当xi 变化时,输出结果就加了一项 wi * 变化量, 若wi 很小接近0,对结果影响并不大,因此会比较平滑。
-
“莱姆大” 正则化项的系数控制了函数的平滑程度,函数不是月平滑越好,有个度,因此有一个系数控制
-
对于偏置b,不用加正则化项是因为 : 正则化使得函数更加平滑,能过滤掉杂色信息,而偏置 b 只能使得函数上下移动,对本来的目的并没有帮助。因此正则化项没有偏置 b 。