数学中的李群初探

李群

直观上的李群

首先李群也是一种降维算法。降维就是为了使用更低维的向量最大程度上表示原来的特征，在机器学习中有很多降维算法：

• PCA(Principal Component Analysis)算法处理的是方形的矩阵(n*n)；

• 奇异值分解 SVD (Singular Value Decomposition) 可以处理任意形状的矩阵(m*n)；

• 李群则可以处理张量,对张量进行降维度。

李群计算流程

李群运动链模型

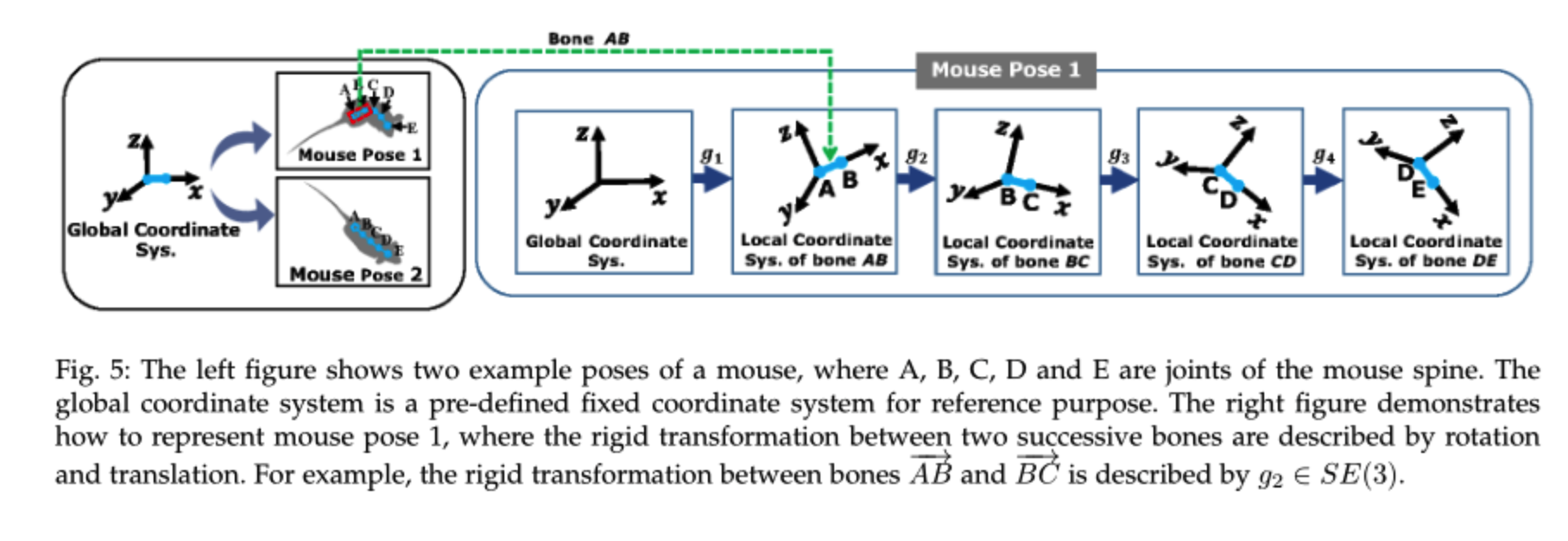
这里以老鼠为例，假设老鼠身上一共有四根骨头，AB,BC,CD,DE，以每根骨头自身作为x轴，单独建立每根骨头的三维坐标系，C的坐标在AB骨头坐标系表示就是：

$$\left[\begin{array}{c}{q}^{\ast }\\ 1\end{array}\right]\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]\ast \left[\begin{array}{c}q\\ 1\end{array}\right]$$

其中，

• q是C在BC三维坐标系下的，形状是**3*1**；

• q^是C在AB坐标系下的坐标，形状是 3*1

• R是旋转矩阵，形状是 3*3

• t是平移矩阵，形状是3*1

• 中间的矩阵就是变换矩阵，整体维度就是 4*1 = 4*4 * 4*1

更一般的坐标变换：

$$\left[\begin{array}{c}{x}^{\ast }\\ 1\end{array}\right]\left[\begin{array}{cc}{R}_i& t_i\\ 0& 1\end{array}\right]\ast \left[\begin{array}{c}x\\ 1\end{array}\right]=g_i\ast \left[\begin{array}{c}x\\ 1\end{array}\right]$$

gi就是上图中的g1，g2…

姿态变换：

两种姿态都可以映射到全局的一个三维坐标系上，就可以进行转换。

旋转矩阵 R

首先R属于三阶特殊正交阵，(满足6个条件) 而本来的维度是9，所以自由度为3，所以可以用一个向量来代替这个旋转矩阵。

所以下面的工作就变成了R的降维工作。

---

预备知识1：斜对角矩阵

$$\mu =({\mu }_1,{\mu }_2,{\mu }_3)$$ $$\hat{\mu }=\left[\begin{array}{ccc}0& -{\mu }_3& {\mu }_2\\ {\mu }_3& 0& -{\mu }_1\\ -{\mu }_2& {\mu }_1& 0\end{array}\right]$$

• 对于任意的μ，总有唯一的μ^与之对应；
• 对于任意的μ^ ，总有唯一的μ与之对应；

预备知识2 ：e^w ^

---

R的变换

直觉理解

• 首先因为旋转矩阵的自由度为3，所以是在3维流形中；
• 在流形曲面处的一个很小的切平面就是李代数，可以用三维坐标表示处原来在流形中的坐标；
• 整个三维流形就是李群