SVM支持向量机

李宏毅老师视频：https://www.bilibili.com/video/BV14W411u78t?from=search&seid=16299976979408181063

知乎讲解 ：https://zhuanlan.zhihu.com/p/49331510

数学完整推导视频：https://www.bilibili.com/video/BV12J41157qV?p=6 （浙大机器学习课程）

文中几张图引自改知乎文章。

Support Vector Machine

概述

整体上，支持向量机是一个分类算法，即寻找能分开两类数据的超平面，并且这个超平面满足距离超平面最近的数据点的到超平面距离最大。

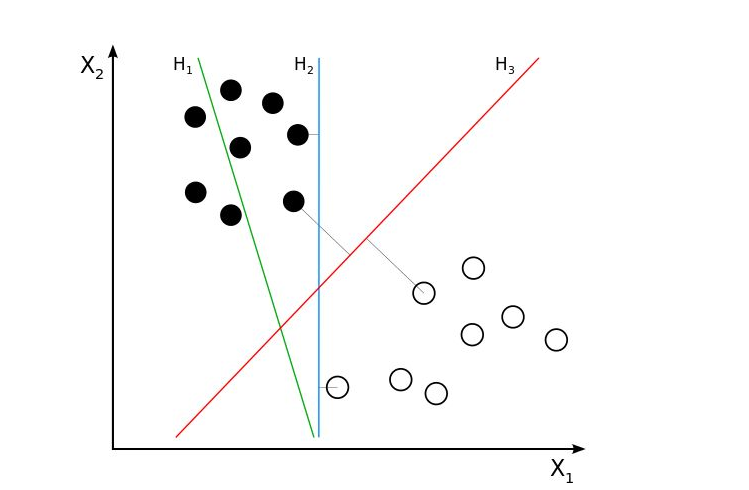
如图，H2和H3都实现了正确的分类，但是SVM会选择H3，因为两类数据中距离H3最近的点的距离比其他所有的点到H3的距离都要大，满足一开始所述的条件。

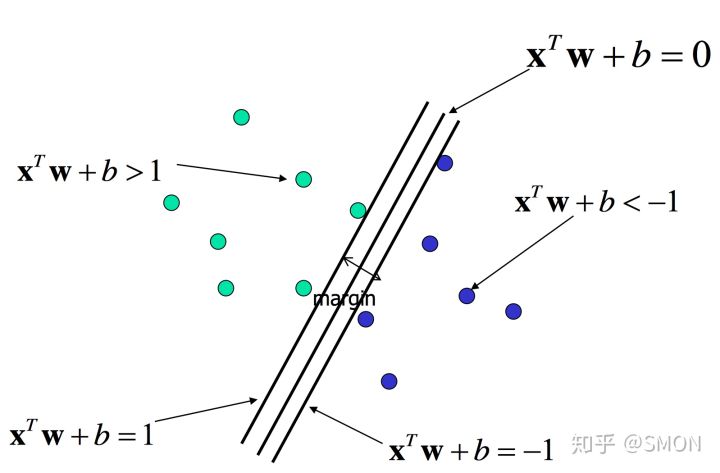
目前求解目标是使得图中margin最大,经过推导得出最终的抽象的公式：

$$mi{n}_{W,b}\frac{1}{2}||W|{|}^2,s.t.y_i\ast (X_i^{T}W+B)>=1$$

这个公式也就是硬匹配规则，简单解释一下：

• yi表示第i个数据的真实类别，取值为 1，-1；
• 第i笔数据真实类别与计算出来的值同号，即保证分类准确的前提下，最大化边界。

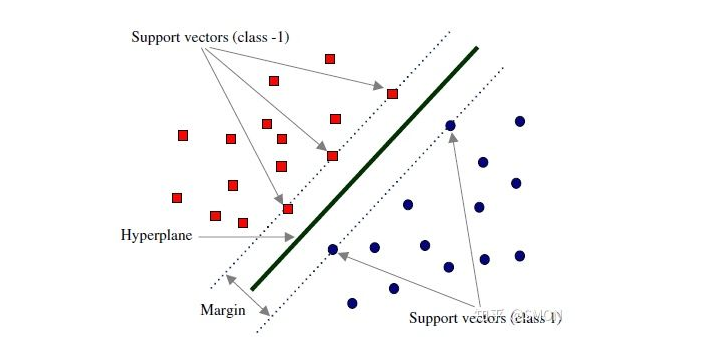
这些处于边界的几个数据点称为支持向量，在决定最佳超平面时只有支持向量起作用，而其他数据点并不起作用。

推导

SVM = Hingle_loss + Kernel_Method

Hingle Loss

$$l(f(x_n),{\hat{y}}_n)=max(0,1-{\hat{y}}_n\ast f(x_n))$$

其中，

$${\hat{y}}_n=1,-1$$

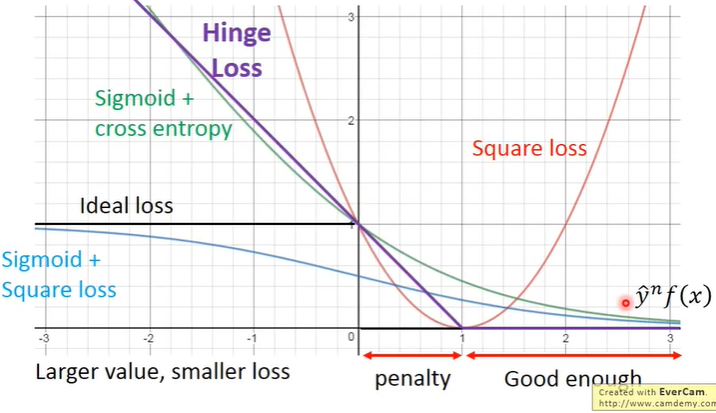
当真值与预测值同号，并且乘积比比正确的好过一段距离，即乘积大于等于1时，loss为0，好过的这段距离即为margin。参考下图：

Linear SVM

• Model:

$$f(x)=\sum _i{w}_i{x}_i+b=\left[\begin{array}{c}w\\ b\end{array}\right]\cdot \left[\begin{array}{c}x\\ 1\end{array}\right]=W^{T}x$$

• Loss function

$$L(f)=\sum _{n}l(f(x_n),{\hat{y}}_n)+\lambda ||w|{|}_2$$

损失函数是一个凸函数，因此可以用梯度下降法来求解，具体看李宏毅老师视频。

这里的SVM损失函数和一开始概述里面提到的目标函数似乎不太一样？经过如下转换，就得到了最初的形式。

最后面1减去了一项，表示是软匹配，不一定能达到1的情况。

Kernel Method

首先，要找的W*(w,b)是数据点的线性组合：

$$w^{\ast }=\sum _n{a}_n^{\ast }\ast x^n$$

为了解释这件事，一般就引入了拉格朗日方法来算一通，这里用另外一种思路：

用梯度下降法求解时，cn(w)由于hingleloss的原因，会有一部分值为0，即不是所有的xn都会对w有影响，w初始化为0时很多数据点对更新w的值毫无用处，即a*是稀疏的。

当a* != 0时，对应的数据点就叫做 Support vector.支持向量机名字也由此得来。

此时w可以换一种形式写：

$$w=\sum _n{a}_n{x}_n=X\alpha$$

故，Model：

$$f(x)=w^{T}x={\alpha }^T{X}^{T}x=\sum _n{a}_n(x_n\cdot x)=\sum _n{a}_{n}K(x_n,x)$$

找一个最好的 α ，最小化损失函数：

$$L(f)=\sum _{n}l(f(x_n),{\hat{y}}_n)=\sum _{n}l(\sum _{n^{\prime }}{a}_{n^{\prime }}K(x_{n^{\prime }},x_n),{\hat{y}}_n)$$

这里不需要知道具体的x，只要能求出K(x,z)的值即可。

Kernel Trick

上述的损失函数如果直接用x，z是不好的，需要用他们的特征。用核方法就不用管他们的 特征是什么样子的。

即两个向量转化为特征向量再求内积是比较麻烦的，直接计算两个向量的内积再求特征会更快。

此时需要定义一个核函数，就可以简化计算。这里的

$$K(x,z)$$

就是一个核函数，可以选取不同的核函数。

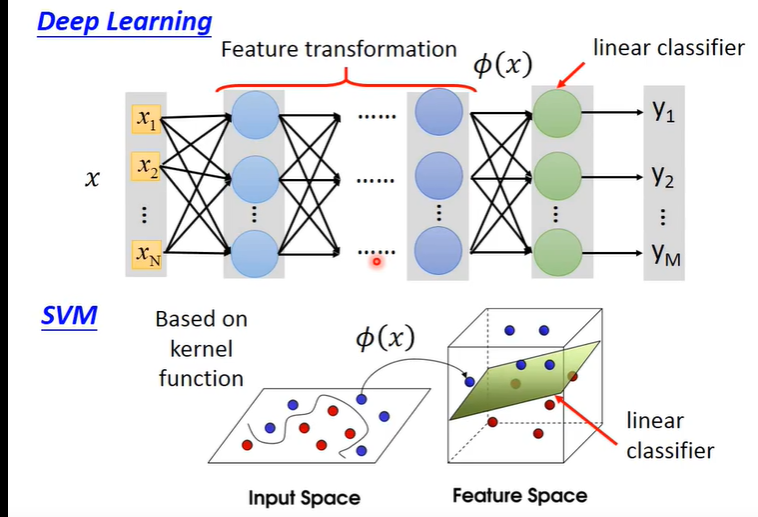
而核函数计算就是把原始数据投影到高维的一个内积，即在做分类时，先把二维数据投影到高维空间，在做一个 线性分类，上图就很明显了。

疑问

• Kernel Trick 是投影到高维的一个计算？
• 逻辑是计算出K，就可以找出α了。而投影到高维只是计算K的一个方法，为什么可以代表svm呢?
• 这些疑问以后再看。

---

2020-6-7日更新：

SVM通过数学理解更加合理！