ResNet-网络分析

Resnet，网络层数非常深，是比较经典的CNN模型，Rennet实现了很深层次的网络的训练。本文主要讨论一下resnet的核心思想。

Universal approximation theorem

万能近似定理，也称通用近似定理，指的是：一个具有两层的神经网络，即一个隐藏层、一个输出层，理论上就可以模拟任何的函数，无论多复杂的函数都可以，只要神经元数量够多。

这个可以理解为 每个神经元都是一个线性的函数，w*x+b，但是当很多神经元组合在一起，就可以模拟出曲线，神经元越多，拟合出的曲线也就会越平滑，这里有点类似于微分，认为曲线是无线可切分的，切到最后会近似成直线，反之，无限多个线性函数自然可以拟合出很平滑的曲线。

但是这只是理论上的，实际上如果真的只采用两层的神经网络，在可行性上就会有很大的问题，比如由于参数量过多可能根本训练不起来。

Residual Block

退化问题

首先，一般认为神经网络层数越深，表达能力会越强。但是实际上，随着神经网络层数加深，却可能出现准确率降低，注意不是过拟合，称为退化问题。因此这种网络结构设计主要是解决了退化问题。而这个方法的出现，也意味着 更深的神经网络可以训练起来了。

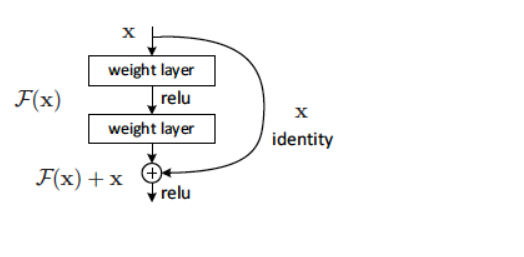
上图便是残差模块。x是输入，经过中间的隐藏层后不直接输出F(x)，而是输入x两一个分支连接到输出出，最终输出F(x)+x,即：

$$H(x)=F(x)+x$$

因为之前的层表现已经很好了，这个多出来的层的本来的学习目标是：让H(x)=x，也就是说尽量让输出不变，但是实际上很难学习到这一点，所以现在的目标就变成了让F(x)->0

为什么说F(x)趋近于0更好训练呢？(借鉴别人)我认为可以从以下两方面考虑：

• Hidden Layer 权重初始化都在0附近，输出的值自然会比较靠近0，因此可能会更好的训练；
• 在该结构中，所有的激活函数都是 RELU, 而relu函数的特性是：小于等于0都置0，这就说明不管怎么样总有一半的概率可以直接置0，不用去计算

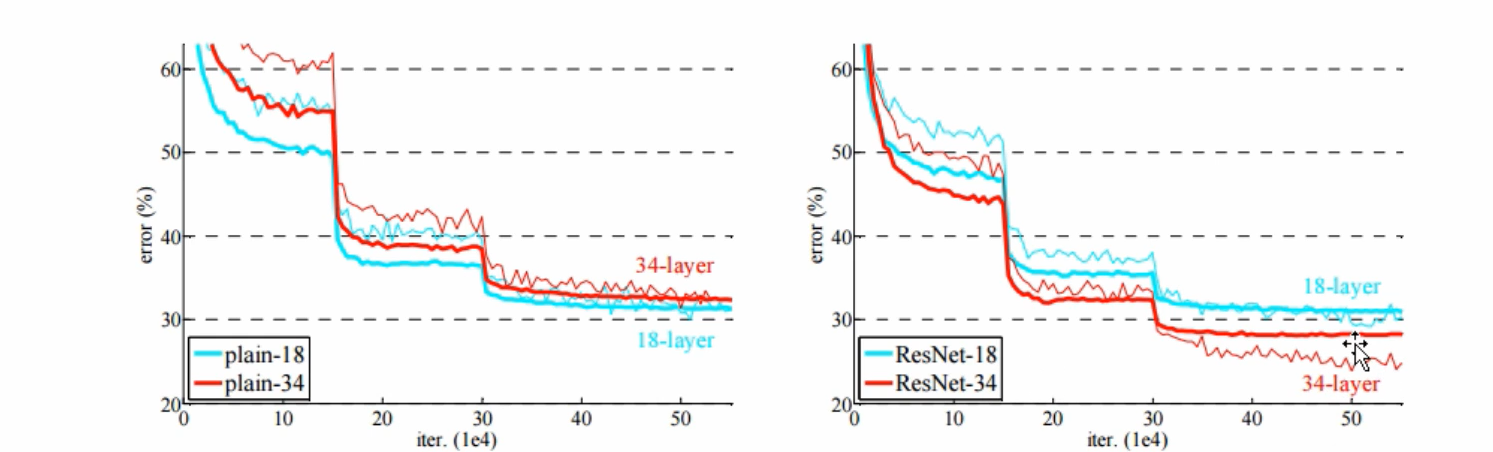
这张图可以看出来，解决了退化问题后，34层的误差明显低于18层

梯度弥散

关于梯度弥散这个问题我纠结了比较久，发现问题在于我把x理解的狭隘了。从数学上理解一下这个问题 ：

$$X_{l+1}=X_l+F(X_l,W_l)$$ $$X_{l+2}=X_{l+1}+F(X_{l+1},W_{l+1})=X_l+F(X_l,W_l)+F(X_{l+1},W_{l+1})$$

故可以推出：

$$X_L=X_l+\sum _{i=1}^{L-1}F(X_i,W_i)$$

此时反向传播计算，假设损失函数是C，此时反向传播要对w求导，就先对后面一个节点求导，然后链式法则再求导W，即：

$$\frac{\partial C}{\partial X_l}=\frac{\partial C}{\partial X_L}\ast \frac{\partial X_L}{\partial X_l}=\frac{\partial C}{\partial X_L}\ast (1+\frac{\partial }{\partial x}\sum _{i=1}^{L-1}F(X_i,W_i))$$

实际上X_l就是一个节点，比如 wx+b，所以对w、b求导就可以求出来了。

此时梯度里面多了一个1，而正是因为这个1的存在，使得梯度存在，可以很容易回流到千层，也就是说算出浅层 的梯度、更细参数。