从 HMM隐马尔可夫模型 到 CRF条件随机域

李宏毅老师课程：https://www.bilibili.com/video/av82565851/

知乎文章：https://zhuanlan.zhihu.com/p/70067113

HMM

整体分析

以词性标注为例，从问题入手，输入X（word），输出Y(tag) ，这里的词性Y是Hidden隐藏的,X是可观测到的Observed。

隐马尔可夫链模型（HMM），着手于建模P(X,Y)即两个序列的联合概率（可以看出来是生成式模型），有条件概率转为联合概率过程如下：

$$\begin{gathered} y=argma{x}_{y}P(y|x) \\ =argma{x}_y\frac{P(x,y)}{P(x)} \\ =argma{x}_{y}P(x,y) \end{gathered}$$

目前为题转化为 穷举所有的y，使得P(x,y)最大。

这里直接计算复杂度会很大 ，所以采用维特比算法 可以求解出这个问题，并且复杂度不是很高。

---

层层深入

这里的P(x,y)如何求解呢？

$$\begin{gathered} P(x,y)=P(x|y)\ast P(y) \\ =\prod _{i=1}^{N}P(x_i|y_i)\ast \prod _{i=1}^{N}P(y_i|y_{i-1}) \end{gathered}$$

其中，

• 第一项条件概率称为发射概率，指从一个词性中抽到某个单词的概率，它基于观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态无关。

  

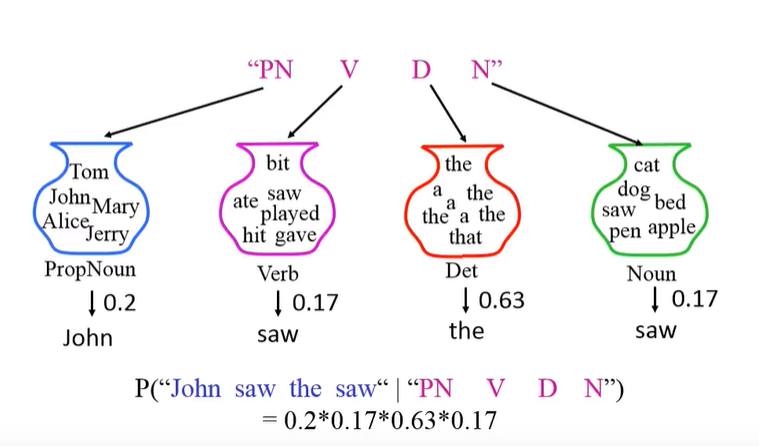
• 第二项则是由**马尔可夫假设**得到，如下图：

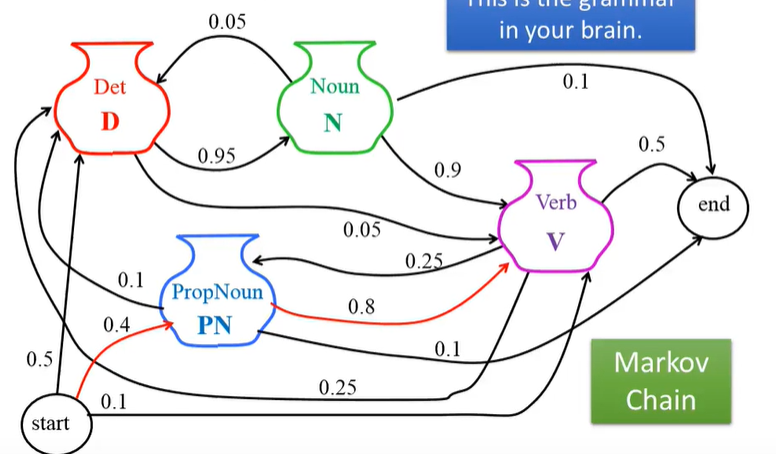
即马尔可夫最终学习的就是发射概率矩阵(x*y)和·转移概率矩阵(y*y),对应起来就是 当前词性产生下一个词性的概率；从当前词性中选出某个词的概率。

---

缺陷

求解时，目标是：

$$P(x,\hat{y})>P(x,y)$$

即真实概率大于预测概率，但是HMM并不会保证这一点。

故HMM存在的一个缺陷是会脑补很多东西，具体可以看李宏毅老师视频。脑部在数据不充分时比较好，但是数据量大依然会凭空捏造，这样效果就不太好。

Condition Random Field 条件随机域

由HMM到CRF

在CRF中，

$$P(x,y)\approx \exp (W\cdot \varphi (x,y))$$

即这两项成正比，其中：

• W是权重向量，从训练数据中学得
• Φ(x,y) 是一个特征向量
• exp()由于不能保证小于1，故是正比于

依然从问题入手，输入X输出Y，求最大化的P(Y|X)：

$$P(y|x)=\frac{P(x,y)}{P(x)}=\frac{P(x,y)}{{\sum }_{y^{\prime }}P(x,y^{\prime })}$$

由上述两者成正比可以推导得：

$$P(x,y)=\frac{\exp (W\cdot \varphi (x,y))}{R}$$

故：

$$\begin{gathered} P(y|x)=\frac{P(x,y)}{{\sum }_{y^{\prime }}P(x,y^{\prime })} \\ =\frac{\exp (W\cdot \varphi (x,y))}{R}\ast \frac{R}{{\sum }_{y^{\prime }}\exp (W\cdot \varphi (x,y^{\prime }))}=\frac{\exp (W\cdot \varphi (x,y))}{{\sum }_{y^{\prime }}\exp (W\cdot \varphi (x,y^{\prime }))} \end{gathered}$$

现在问题来了，为什么P(x,y)可以写成后面那一项？······具体推导省略，过程可以看李宏毅老师视频

其中，

• 权重向量W可以对应为HMM中计算的概率取log
• Ns,t(x,y)则是这一对出现的次数，记作Φ(z,y)

Φ(x,y)特征向量由两部分组成，一部分是词性产生词性的pair的次数，另一部分是词性中产生相应词汇的次数，形状如下：

---

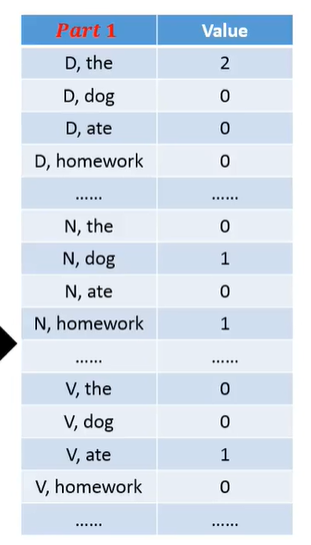
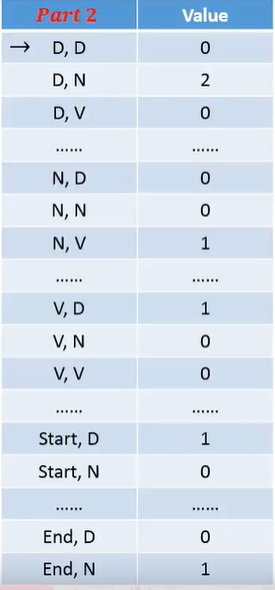
Training

上述特征向量Φ可以自定义，故要求的参数即为权重w，即：

$$W^{\ast }=\arg ma{x}_{w}O(w)$$

其中，对象方程为：

$$O(w)=\sum _{n=1}^N\log P({\hat{y}}_n|x_n)$$

其中：

$$\log P({\hat{y}}_n|x_n)=\log P(x_n,{\hat{y}}_n)-\log \sum _{y^{\prime }}P(x_n,y^{\prime })$$

所以目标就是最大化上述公式的前一项，最小化上述公式后一项。而前一项是观测出现的概率，后一项是没有观测到即随机组合出现的概率，这在直观上也是正确的。

然后采用梯度下降法来求解：

即：

$$\Delta O(W)=\varphi (x_n,y_n)-\sum _{y^{\prime }}P(y^{\prime }|x_n)\varphi (x_n,y^{\prime })$$

由于是最大化所以采用 Stochastic Gradient Ascent 更新参数：

$$w=w+\eta (\varphi (x_n,y_n)-\sum _{y^{\prime }}P(y^{\prime }|x_n)\varphi (x_n,y^{\prime }))$$

在Inference时，

$$\begin{gathered} y=argma{x}_{y}P(y|x) \\ =\arg ma{x}_y\frac{P(x,y)}{P(x)} \\ =\arg ma{x}_{y}P(x,y) \\ =\arg ma{x}_y\exp (W\cdot \varphi (x,y))=\arg ma{x}_{y}W\cdot \varphi (x,y) \end{gathered}$$

CRF与HMM

CRF在增加标签对出现的概率的同时，也减小了其他随意组合的对出现的概率，这就抑制了HMM容易脑补的问题。

HMM是生成式模型，最终在求解联合概率；

CRF实际上是判别式模型，从Inference可以看出，是直接求出了条件概率。