Cross Entropy 的前世今生

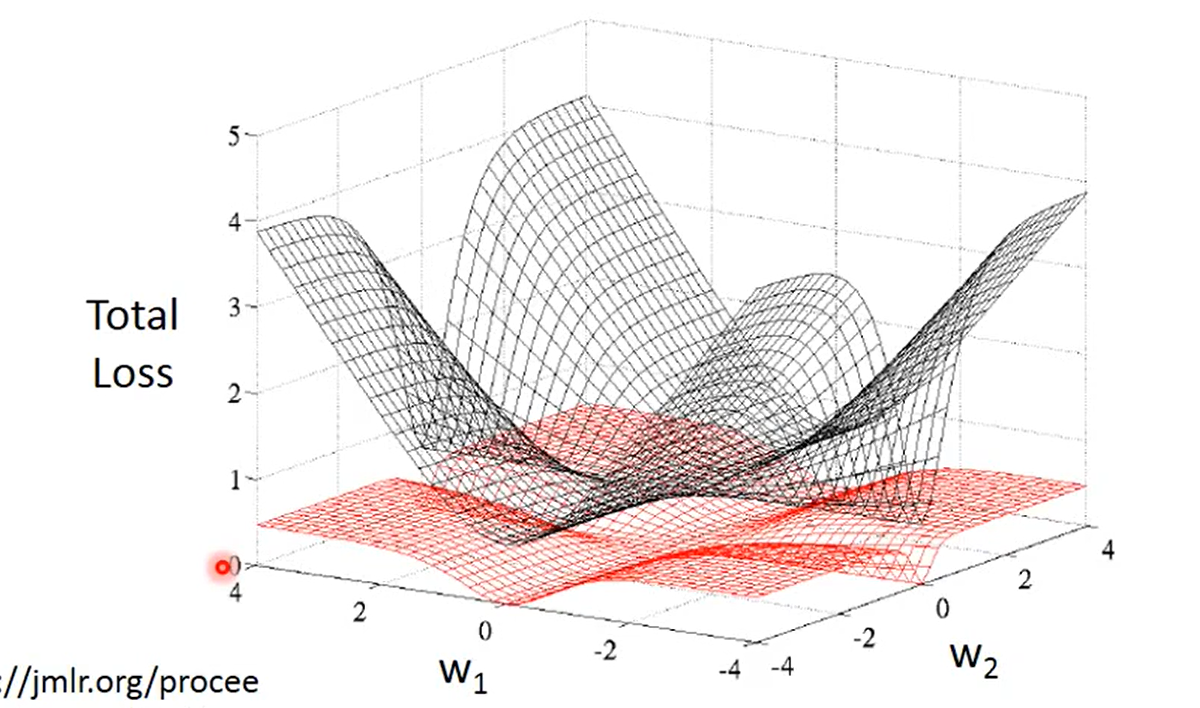
Deep Learning 中可以分为分类问题和回归问题，而分类问题也可以转化为回归问题，具体可以看Classification 这篇文章。回归问题一般用均方误差作为损失函数(显而易见)，而分类问题一般则用交叉熵作为损失函数，这是为什么？这一切要从信息熵说起…

信息熵&交叉熵

https://www.zhihu.com/question/41252833/answer/195901726 这篇知乎文章很通俗的解释了交叉熵的概念，总结一下：

信息论中，使用信息熵来对概率分布进行量化。**信息熵代表的是随机变量或整个系统的不确定性，熵越大，随机变量或系统的不确定性就越大。**根据真实分布，我们能够找到一个最优策略，以最小的代价消除系统的不确定性，而这个代价大小就是信息熵，记住，信息熵衡量了系统的不确定性，而我们要消除这个不确定性，所要付出的【最小努力】（猜题次数、编码长度等）的大小就是信息熵。

但是并不是每次都知道真实分布，在深度学习中是不知道真实的分布的，这时候就引入交叉熵：交叉熵，其用来衡量在给定的真实分布下，使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。

交叉熵公式如下：

$$\sum _{k=1}^N{p}_k\ast lo{g}_2^{{\frac{1}{q}}_k}$$

其中(https://www.zhihu.com/equation?tex=p_k) 表示真实分布，(https://www.zhihu.com/equation?tex=q_k) 表示非真实分布。交叉熵最小值就是采用真实分布预测出来的结果，此时

交叉熵 == 信息熵 , 因此在机器学习中要最小化交叉熵，此时就最近真最佳策略。

深度学习中的交叉熵

举一个最简单的例子，y = w * x + b，目标是输入为1输出为0.经过 σ 函数进行二分类,首先定义损失函数(先用均方误差)：

$$C=(y-a{)}^2/2$$

其中y为真实值，a为我们算出来的值，因为要经过 σ 函数进行分类，所以 a = σ (w*x + b),令 z = w*x + b,a = σ(z)，用梯度下降法求w，b就需要先对其求微分，用到链式求导法则：

$$\begin{gathered} \frac{\partial C}{\partial w}=\frac{\partial C}{\partial a}\ast \frac{\partial a}{\partial w} \\ \partial C/\partial a=a-y \\ \partial a/\partial w={\sigma }^{\prime }(z)\ast x \end{gathered}$$

此时设x=1，相应的y=0，

$$\begin{gathered} \partial C/\partial w=a\ast {\sigma }^{\prime }(z) \\ \partial C/\partial b=a\ast {\sigma }^{\prime }(z) \end{gathered}$$

因为经过了sigmoid函数，所以当z较大时，梯度很小，此时会发生梯度弥散,更新参数会很慢，那么如何加快参数更新？交叉熵是凭空出现的吗?若果没有σ这项：

$$\begin{gathered} \partial C/\partial w_i=(a-y)\ast x_i \\ \partial C/\partial b=a-y \end{gathered}$$

考虑之前的推导：

$$\partial C/\partial w_i=\frac{\partial C}{\partial a}\ast {\sigma }^{\prime }(z)x_i=\frac{\partial C}{\partial a}\ast a(1-a)x_i$$

令（6）和（5）相等可得出:

$$\partial C/\partial a=\frac{a-y}{a(1-a)}$$

此时用积分求出原函数即：

$$C=-[y\ln a+(1-y)\ln (1-a)]+constant$$

这就是二分类中交叉熵的函数形式，伯努利二项分布。

由此可以知道交叉熵的来源、推导。也解释了分类问题为什么用交叉熵作为损失函数，简而言之，交叉熵作为损失函数，消去了σ这一项，从而变成线性的，解决了更新参数很慢的问题，这时候再引用一张之前的图就一目了然了：