Contrastive Loss (对比损失)分析

定义及分析

Contrastive loss 即对比损失，其表达式为：

$$L=\frac{1}{2N}\sum _{n=1}^{N}y{d}^2+(1-y)max(margin-d,0{)}^2$$

其中，

• y表示标签值，取值为 1，0;

• margin是人为定义的边界距离；

• d表示两个样本的欧氏距离

输入为 ( dataA, dataB, label )

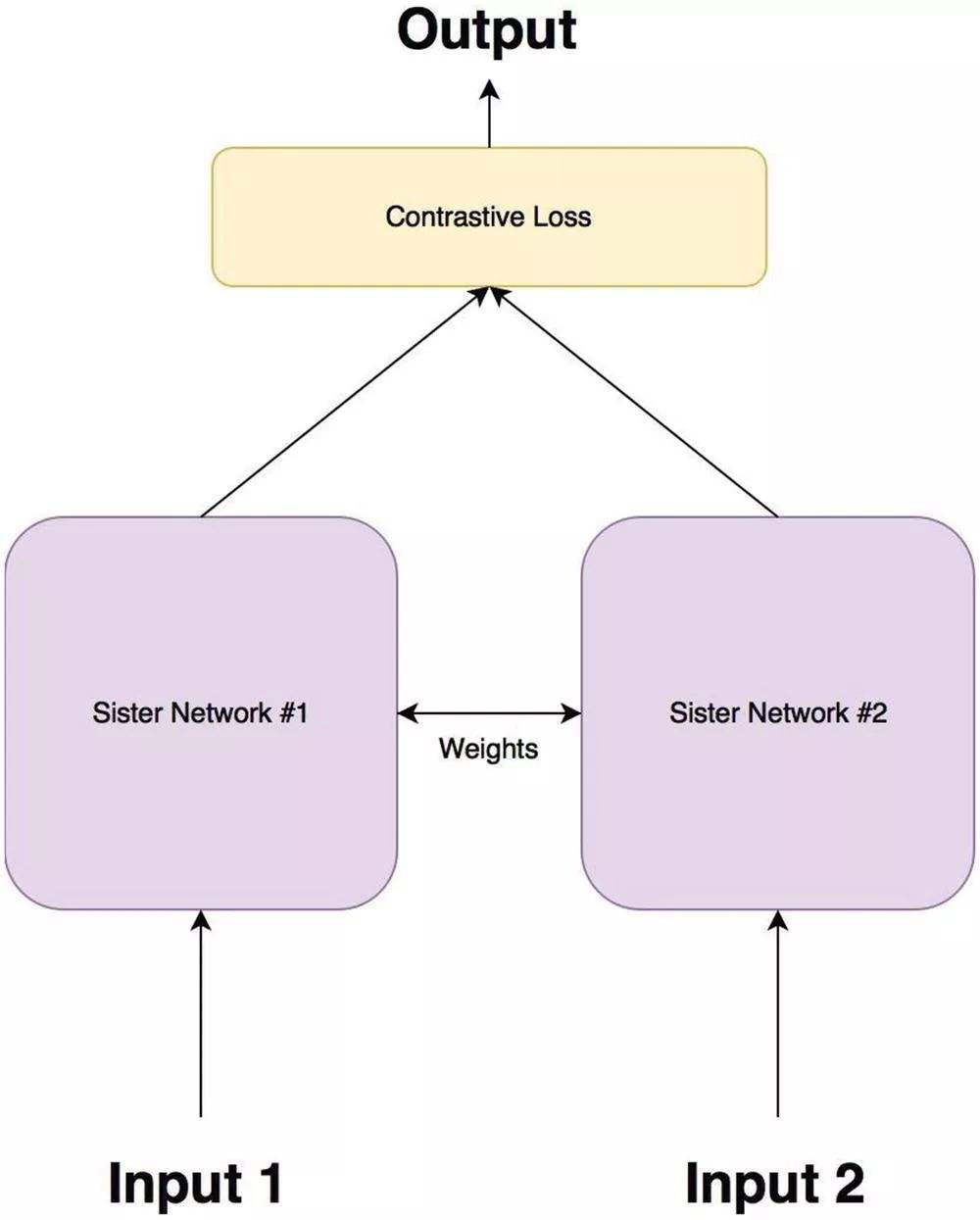
该损失函数可以有效的处理孪生神经网络中的paired data的关系，具体逻辑是：

• 若一对数据是同一组，那么label = 1 即y = 1 ，只有前半部分起作用，后半部分值为0；此时最小化loss, 两者的欧氏距离变小，就会使两者更相似；
• 若一对数据非同一组，那么label = 0 即y = 0， 只有后半部分起作用，前半部分值为0，此时最小化损失函数，即最小化margin - d, 就等于最大化d ,即两者的欧氏距离变大，更不相似

梯度求解

y = 1时，

$$L=\frac{1}{2N}\sum _{n=1}^{N}y{D}^2=\frac{1}{2N}\sum _{n=1}^N(||x_1-x_2|{|}_2){)}^2$$ $$\frac{\partial L}{\partial X}=\frac{\partial D_w}{\partial X}=||x_1-x_2|{|}_2\ast \partial D/\partial X$$

此处省略，以后补充

代码实现

# ------------------------------------------------------------------------------
# # @Time    : 2020/5/17 上午 11:19
# # @Author  : fry
# @FileName: clac.py
# ------------------------------------------------------------------------------
'''
计算欧式距离
'''
 
import torch
 
def euclidean_dist_vector(x, y):
    '''
 
    :param x: [100]
    :param y: [100]
    :return:
    '''
    dist = torch.sqrt(torch.sum(torch.pow((x-y), 2)))
    return dist
 
def euclidean_dist(x, y):
    """
    Args:
      x: pytorch Variable, with shape [m, d]
      y: pytorch Variable, with shape [n, d]
    Returns:
      dist: pytorch Variable, with shape [m, n]
    """
 
    m, n = x.size(0), y.size(0)
    # xx经过pow()方法对每单个数据进行二次方操作后，在axis=1 方向（横向，就是第一列向最后一列的方向）加和，此时xx的shape为(m, 1)，经过expand()方法，扩展n-1次，此时xx的shape为(m, n)
    xx = torch.pow(x, 2).sum(1, keepdim=True).expand(m, n)
    # yy会在最后进行转置的操作
    yy = torch.pow(y, 2).sum(1, keepdim=True).expand(n, m).t()
    dist = xx + yy
    # torch.addmm(beta=1, input, alpha=1, mat1, mat2, out=None)，这行表示的意思是dist - 2 * x * yT
    dist.addmm_(1, -2, x, y.t())
    # clamp()函数可以限定dist内元素的最大最小范围，dist最后开方，得到样本之间的距离矩阵
    dist = dist.clamp(min=1e-12).sqrt()  # for numerical stability
    return dist
 
 

# ------------------------------------------------------------------------------
# # @Time    : 2020/5/11 下午 7:52
# # @Author  : fry
# @FileName: MatchLoss.py
# ------------------------------------------------------------------------------
 
import numpy as np
import torch
import torch.nn as nn
from utils.clac import euclidean_dist,euclidean_dist_vector
# match loss function
 
class ContrastiveLoss(nn.Module):
    """
    Contrastive loss function.
 
    Based on:
    """
 
    def __init__(self, margin=1.2):
        super(ContrastiveLoss, self).__init__()
        self.margin = margin
 
 
    def check_type_forward(self, in_types):
        assert len(in_types) == 3
        #[1,1,10,10] [1,1,10,10] [10]
        x0_type, x1_type, y_type = in_types
        assert x0_type.size() == x1_type.shape
        # assert x1_type.size()[1] == y_type.shape[0]
        # assert x1_type.size()[0] > 0
        assert x0_type.dim() == 4
        assert x1_type.dim() == 4
        # assert y_type.dim() == 1
 
    def forward(self, x0, x1, y):
 
        # self.check_type_forward((x0, x1, y))
 
        data_1 = x0 # [1,10,10]
        data_2 = x1 # [1,10,10]
        # euclidian distance
        distance = euclidean_dist_vector(data_1, data_2)
        # distance = euclidean_dist(data_1, data_2)
        md = self.margin - distance
        dist = torch.clamp(md, min=0.0)
        loss = y * torch.pow(distance, 2) + (1-y)*torch.pow(dist, 2)
        loss = torch.mean(loss/2)
        # loss = torch.sum(loss) / 2.0
        return loss
# if __name__ == '__main__':
#     citer = ContrastiveLoss()
#     a = torch.randn(10,10)
#     b = torch.randn(10,10)
#     y = torch.ones(1)
#     loss = citer(a,b,y)
#     print(loss)