Auto Encoder in DeepLearning

VAE部分公式推导省略的可以观看李宏毅老师的课：https://www.bilibili.com/video/av9770190?p=18

Back Ground

首先自编码器的意义是什么呢？

以CV举例，在影像处理中，人脸识别一张普通的200*200像素的图，就有40000维向量要处理，显然不实际，因此如果可以有一个编码器可以输入一张图，输出一个30维的向量；再将这个30维向量输出成200*200的图，尽量与原图接近。也就是说30维的向量代表了40000维的图，并且尽量保持图片特征、不失真，这就是自编码器的应用。

Auto Encoder

最初的 Auto Encoder设计结构如下图：

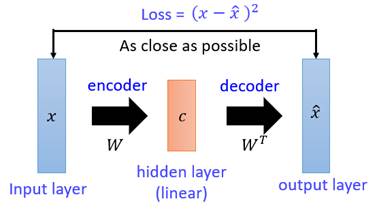
只要让输出尽可能的接近输入即可，然后改造成深度自编码器，如下：

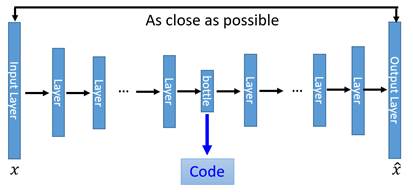
loss依然是最初的。这便是Auto Encoder

Problem in Auto Encoder

首先，Auto Encoder存在一个问题，它把所有训练的图片都是对应到了一个高维空间中的一个点，可以这么理解，本来图像是40000维空间的一个点，经过编码变成30维空间的一个点，如果采样正好采了这个点，则可以比较精确的用解码器还原图像；但是如果在30维空间中，采样到了一个从未训练过的点，那么解码器就大概率只会解码出一堆噪音，如下图：

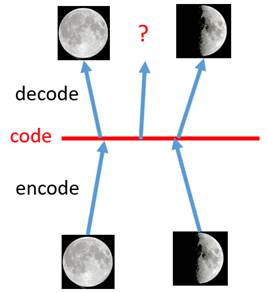
如果采样到 code中间未训练过的点，解码出来的图像就不像是一张真实图像，会是一堆乱码，而VAE做的事情就是每张图片不在是对应一个点，而是一个区间，在这个区间内都可以解码出这张图片，如下图：

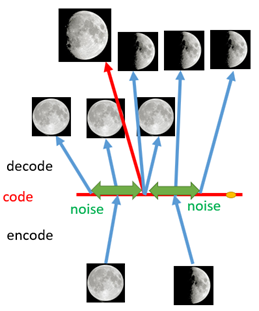
这就引入了VAE.

Variance Auto Encoder(VAE)

先看一下VAE的整体架构：

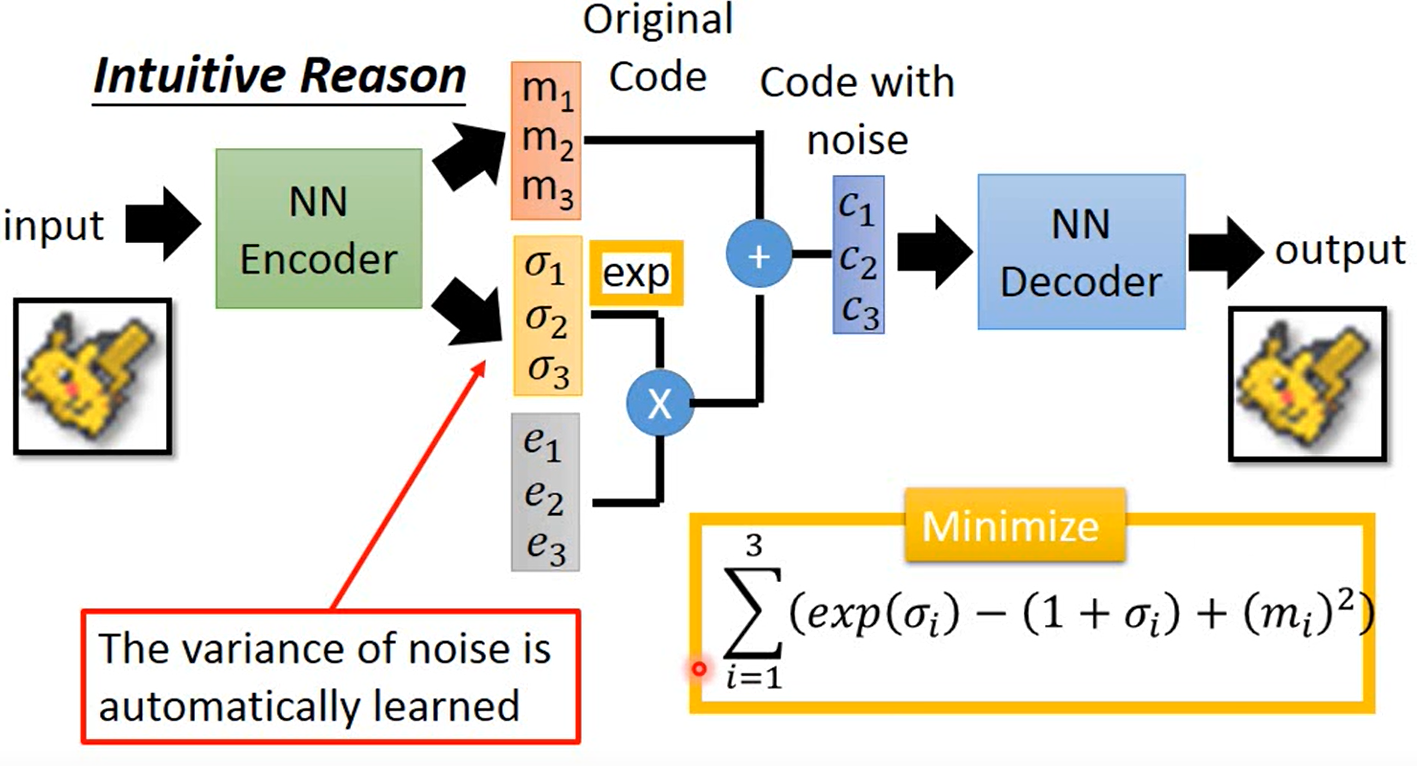
首先是输入经过一个编码器，产生一组m，一组σ，然后一组e是从高斯分布采样的，即：

$$m_i+\exp ({\sigma }_i)+e_i=c_i$$

也就是原始编码加上噪音，而σ则是控制噪音的方差，即$\exp ({\sigma }_i)$就是噪音的方差，是自动学习的；同时损失函数在原来的基础上，加上了上图右下角一项。

直观上，如果不加限制的让机器自己去学习，那么机器肯定会认为噪音对原图像干扰越小越好，于是会给exp(σ)赋值为0或者很接近0的数，但是这也就失去了意义。因此加上这一项，$\exp ({\sigma }_i)-(1+{\sigma }_i)$的最小值在σ=0时得到最小值，也就是说σ=0loss最小，此时方差=1,所以机器自己学习就不会让Variance太小；$m_i^2$可以认为是L2正则化。这就是直观上VAE这样设计的原理，下面从数学上理解VAE的原理。

VAE的原理

首先，我们的工作任务是可以采样到需要的图像，也就是要估计原始图像的概率分布P(X),如果知道了原始图像的分布，那么我们只要让我们的生成的图像分布尽量接近原始图像也就是计算它们的KL散度即可。所以为题转化为求P(X).

高斯混合模型认为，任何一个分布都可以由多种高斯分布混合(加权和)而成。则此时；

$$\begin{gathered} P(X)=\sum _{m}P(m)\ast P(x|m) \\ x|m\approx N({\mu }_m,{\sigma }_m) \end{gathered}$$

这件事更像是对图像做了一个分类，我们所看到的x都来自于某一类，这是不好的，更好的方法应该是用一个向量来表示图像。

则此时引出了z，z是一个隐向量，是服从高斯分布的；向量的每一个维度对应图像的某一些特征。注意，这里之所以z取高斯分布，是因为逻辑上说，没有特色的东西占多数，图像每种属性的分布其实大概率是服从高斯分布的，因此z取高斯分布也是比较合理的，但是z可以是任何分布。

同时，z有无穷多个，是连续的，不再是高斯混合模型那样有固定个z；每一个z对应的均值μ、方差σ都是由神经网络学来的。

所以此时，

$$\begin{gathered} P(X)={\int }_{z}P(z)\ast P(X|z)dz \\ P(z)\approx N(0,1) \\ X|z\approx N(\mu (z),\sigma (z)) \end{gathered}$$

真正要求的就是μ(z)、σ(z)，最大化P(X):

$$L=\sum _X\log P(X)$$

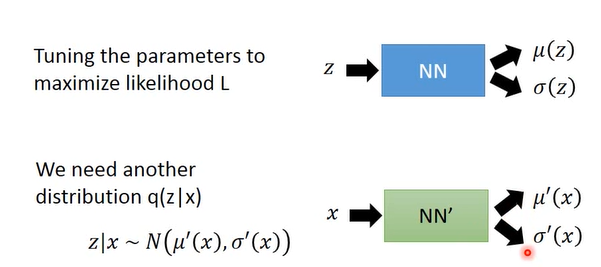
所以，此时z经过一个伸进和网络输出均值和方差，目的是最大化L；这时候需要引入另外一个分布q(z|x),也就是输入图像，提取它的高斯分布；所以，上图中蓝色的就是Decoder，绿色的就是Encoder。然后继续用数学推导：

注意以下公式推导有跳步，具体可以看一下李宏毅老师的视频讲解。

$$\log P(x)={\int }_{z}q(z|x)\log P(x)dz={\int }_{z}q(z|x)\log \frac{P(z,x)}{q(z|x)}dz+KL(q(z|x)||p(z|x))$$

其中，KL散度一项大于等于0，故前面的一项就是$\log P(x)$的下限(lower bound).这个下限记为Lb:

$$L_b={\int }_{z}q(z|x)\log \frac{P(z,x)}{q(z|x)}dz={\int }_{z}q(z|x)\log \frac{P(z)\ast P(x|z)}{q(z|x)}dz$$

则原式化作:

$$\log P(x)=L_b+KL(q(z|x)||p(z|x))$$

这里就真正的体现了VAE的精妙之处：

本来是要寻找P(x|z)来最大化L，但是现在需要同时寻找P(x|z)、q(z|x)两项，来最大化Lb，从而最大化L。

q分布实际上与 log P(x) 是无关的，log P(x)至于P分布有关。所以q无论取什么值，log P(x) 都不变，如下图：

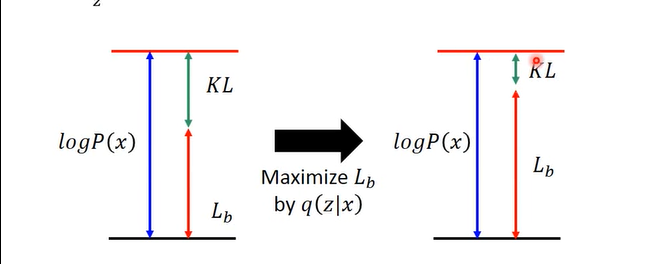
所以当P固定，q最大化Lb时，KL会越来越小，最后消失不见，也就是q(z|x)和p(z|x)的分布完全相同，此时在上升下限，Likelyhood也会最大化。所以也就是说损失函数中实际起作用的就是Lb这一项。

所以此时，就是寻找P(x|z)、q(z|x)最大化Lb来最大化似然估计，同时顺便会找到q(z|x)相似于p(z|x)。

$$L_b={\int }_{z}q(z|x)\log \frac{P(z,x)}{q(z|x)}dz=-KL(q(z|x)||P(z))+{\int }_{z}q(z|x)\log P(x|z)dz$$

此时最大化Lb，也就是要最小化q(z|x)和P(z)的相似度，其中q是一个神经网络，用来提取输入x所服从的高斯分布，所以这里最小化的散度就是要调节q所对应的神经网络，让它产生的高斯分布与z这个高斯分布越接近越好，最小化散度这一项可以推导为：

$$KL(q(z|x)||P(z))=\sum _{i=1}^3(\exp ({\sigma }_i)-(1+{\sigma }_i)+(m_i{)}^2)$$

这就是文章一开始提到的VAE架构中新增的需要最小化的损失函数。

而Lb另外一项积分也要最大化，即：

$$\max {\int }_{z}q(z|x)\log P(x|z)dz$$

直观上就是从q中采样一个z分布，使得在在z分布下采样到的x的概率越大越好。这实际上就是Auto Encoder在做的事情。

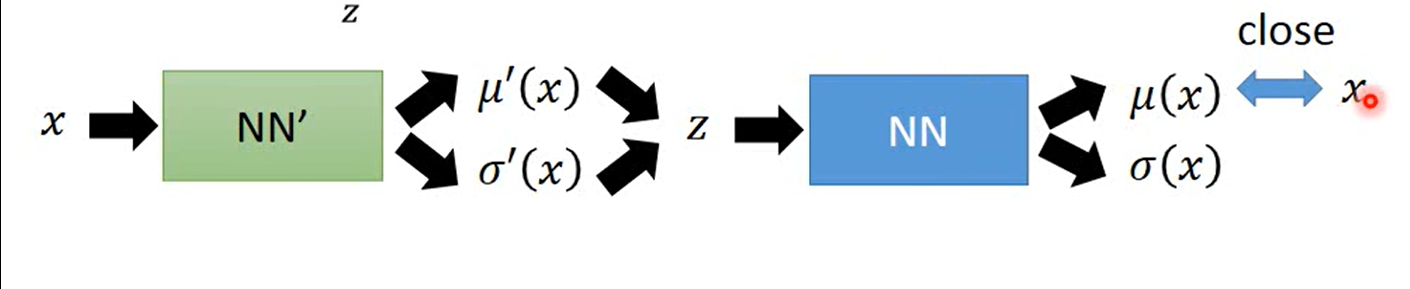
通俗的描述一下，就是说，首先q会从输入图像x中采样出一个(Normal Distribution )z,然后要最大化z分布产生x的概率，就是会把z作为NN的输入，输出一组高斯分布，使得这个高斯分布产生x的概率最大 。所以现在就是如何让这组高斯产生的x概率最大。

实际上在训练时，我们不会取考虑方差，只需要让Decoder输出的均值**(mean)μ=x(Input)**即可，因为高斯分布在均值μ处采样的可能性最大，所以只需要让x=μ即可。也就是说这一部分就是让输入的x与输出尽可能的接近。

同时，因为Encoder和Decoder的输出3都是一组分布，即现在图片对应的是一个分布，所以也就解决了把图片对应到了一个点上的问题，也就解决了Auto Encoder的存在的问题。

所以Lb这两项合起来，就是文章一开始提到的VAE的两个损失函数。所以说VAE就精妙在损失函数的设计上面。

妙哉妙哉！