最小二乘法和梯度下降法

最小二乘法是用来最小化误差函数从而寻找函数得最佳参数的一种方法，学习的时候最小二乘法与梯度下降法我感觉很类似，所以来记录一下。

参考文章：https://zhuanlan.zhihu.com/p/109986821

最小二乘法推导

首先，一元线性回归的最小二乘法推导比较容易，上述知乎也有链接，这里直接给出结论：

$$\begin{gathered} y=Wx+b \\ x=x_1,x_2,...x_m \end{gathered}$$ $$\{\begin{array}{l}W=\frac{{\sum }_{i=1}^m(x_i-\bar{x})\ast (y_i-\bar{y})}{{\sum }_{i=1}^m(x_i-\bar{x}{)}^2}\\ b=\bar{y}-W\ast \bar{x}\end{array}$$

对于多元线性回归，采用矩阵求解：同样直接给出结论

$$y=X\beta$$

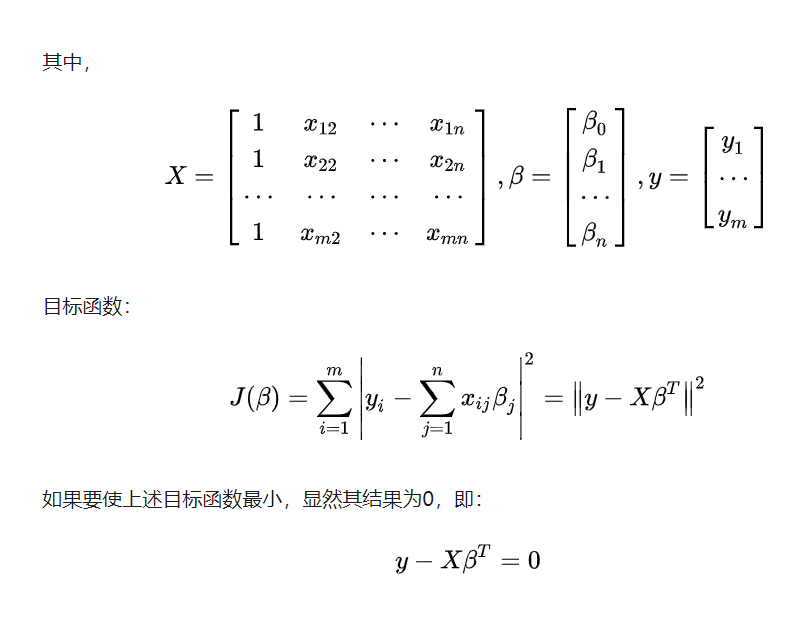
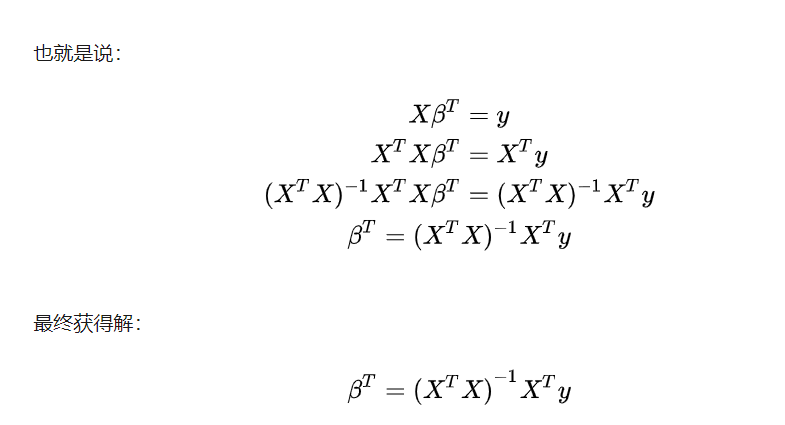
两者区别

由上述可以看出，

最小二乘法：

• 可以直接求矩阵求逆一步到位，求出所的参数，求的全局最优解，无需迭代；
• 但是只适用于线性回归模型，并且矩阵复杂时计算复杂度高

梯度下降法：

• 需要设置学习率进行一步步迭代，求得局部最小值或者是全局最优解
• 适用于任何模型，只要是凸函数均可以求求出解

思考

这里想起来分类为什么不适合用最小二乘法求解？

最小二乘法(y-y-true)^2有个平方，对于离群的点平方会很致命，尽量拟合数据就会导致错误出现

---

2020年4月7日夜